题目内容
11.如图1,△ABC和△CDE都是等腰直角三角形,∠C=90°,将△CDE绕点C逆时针旋转一个角度α(0°<α<90°),使点A,D,E在同一直线上,连接AD,BE.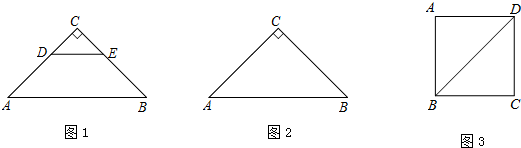
(1)①依题意补全图2;
②求证:AD=BE,且AD⊥BE;
③作CM⊥DE,垂足为M,请用等式表示出线段CM,AE,BE之间的数量关系;
(2)如图3,正方形ABCD边长为$\sqrt{5}$,若点P满足PD=1,且∠BPD=90°,请直接写出点A到BP的距离.
分析 (1)①根据旋转的特性画出图象;②由∠ACD、∠BCE均与∠DCB互余可得出∠ACD=∠BCE,由△ABC和△CDE都是等腰直角三角形可得出AC=BC、DC=EC,结合全等三角形的判定定理SAS即可得出△ADC≌△BEC,从而得出AD=BE,再由∠BCE=∠ADC=135°,∠CED=45°即可得出∠AEB=90°,即证出AD⊥BE;③依照题意画出图形,根据组合图形的面积为两个三角形的面积和可用AE,BE去表示CM;
(2)根据题意画出图形,比照(1)③的结论以及利用全等三角形的性质,套入数据即可得出结论.
解答 解:(1)①依照题意补全图2,如下图(一)所示.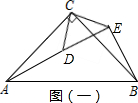
②证明:∵∠ACD+∠DCB=∠ACB=90°,∠BCE+∠DCB=∠DCE=90°,
∴∠ACD=∠BCE.
∵△ABC和△CDE都是等腰直角三角形,
∴AC=BC,DC=EC.
在△ADC和△BEC中,有$\left\{\begin{array}{l}{AC=BC}\\{∠ACD=∠BCE}\\{DC=EC}\end{array}\right.$,
∴△ADC≌△BEC(SAS),
∴AD=BE,∠BEC=∠ADC.
∵点A,D,E在同一直线上,△CDE是等腰直角三角形,
∴∠CDE=∠CED=45°,∠ADC=180°-∠CDE=135°,
∴∠AEB=∠BEC-∠CED=135°-45°=90°,
∴AD⊥BE.
③依照题意画出图形,如图(二)所示.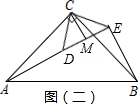
∵△CDE为等腰直角三角形,
∴DE=2CM.
又∵AD=BE,
∴AE-BE=2CM.
∵S△ABC+S△EBC=S△CAE+S△EAB,
即$\frac{1}{2}$AC•BC+$\frac{1}{2}$BE•CM=$\frac{1}{2}$AE(CM+BE),
∴AC2-AE•BE=CM(AE-BE),
∴CM=$\sqrt{\frac{A{C}^{2}-AE•BE}{2}}$.
(2)依照题意画出图形(三).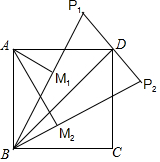
其中AB=$\sqrt{5}$,DP=1,BD=$\sqrt{2}$AB=$\sqrt{10}$,
由勾股定理得:BP=$\sqrt{B{D}^{2}-D{P}^{2}}$=3.
结合(1)③的结论可知:
AM1=$\sqrt{\frac{A{B}^{2}-BP•DP}{2}}$=$\sqrt{\frac{5-3×1}{2}}$=1;
∵∠ABM1+∠CBM1=90°,∠ABM1+∠BAM1=90°,
∴∠CBM1=∠BAM1.
∵∠ABM2=∠CBM1,
∴∠ABM2=∠CBM1.
在△ABM1和△BAM2中,$\left\{\begin{array}{l}{∠AB{M}_{2}=∠CB{M}_{1}}\\{∠A{M}_{1}B=∠B{M}_{2}A=90°}\\{AB=BA}\end{array}\right.$,
∴△ABM1≌△BAM2(AAS),
∴AM2=BM1=$\sqrt{A{B}^{2}-A{{M}_{1}}^{2}}$=2.
故点A到BP的距离为1或2.
点评 本题考查了旋转的性质、全等三角形的判定及性质、三角形的面积公式、角的计算以及勾股定理,解题的关键:(1)①结合题意画出图形;②找出△ADC≌△BEC;③利用分割法求组合图形的面积;(2)利用类比法借助(1)③的算式求出结论.本题属于中档题,(1)①②难度不大;③难度不小,此处用到了分割组合图形求面积来找等式,该小问处切记线段AC当成已知量;(2)利用类比的方法套入(1)③的算式即可.解决该题型题目时,画出图形,注意数形结合是关键.

 的两根,则k的值为______.
的两根,则k的值为______.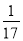 C. ﹣17 D. ﹣
C. ﹣17 D. ﹣
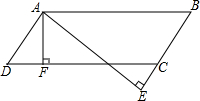 如图,过?ABCD的顶点A分别作AF⊥DC于F,AE⊥BC交BC的延长线于点E,若AE=3.5cm,AF=2.8cm,∠EAF=30°,则AB=7cm,AD=5.6cm.
如图,过?ABCD的顶点A分别作AF⊥DC于F,AE⊥BC交BC的延长线于点E,若AE=3.5cm,AF=2.8cm,∠EAF=30°,则AB=7cm,AD=5.6cm.