题目内容
1.若二次三项式kx2+2x-5可以在实数范围内因式分解,则k的取值范围是k≥-$\frac{1}{5}$.分析 由多项式可以在实数范围内因式分解可知△≥0,解不等式可得.
解答 解:∵kx2+2x-5可以在实数范围内因式分解,
∴△=22-4•k•(-5)≥0,
解得:k≥-$\frac{1}{5}$,
故答案为:k≥-$\frac{1}{5}$.
点评 本题主要考查了实数范围内分解因式,二次三项式在实数范围内能分解因式,即方程有解,也就是△≥0,读懂题意是解答本题的关键.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案
相关题目
12.多项式5mx3+25mx2-10mxy各项的公因式是( )
| A. | 5mx2 | B. | 5mxy | C. | mx | D. | 5mx |
16.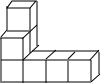 如图,是由相同小正方形组成的立方体图形,它的左视图为( )
如图,是由相同小正方形组成的立方体图形,它的左视图为( )
 如图,是由相同小正方形组成的立方体图形,它的左视图为( )
如图,是由相同小正方形组成的立方体图形,它的左视图为( )| A. | 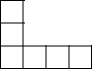 | B. | 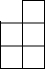 | C. | 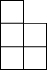 | D. |  |
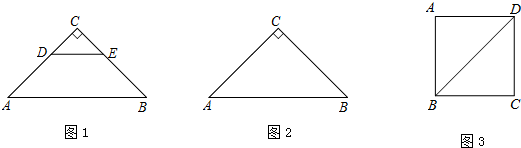
 如图,将三角形ABC沿BC方向平移得到三角形DEF,若CF=2cm,则BE=2cm.
如图,将三角形ABC沿BC方向平移得到三角形DEF,若CF=2cm,则BE=2cm.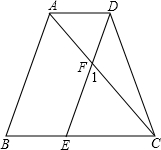 如图,已知AD∥BC,∠1=∠ACB,AC平分∠DAB,试说明:AB∥DE.
如图,已知AD∥BC,∠1=∠ACB,AC平分∠DAB,试说明:AB∥DE.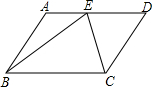 如图,点E是?ABCD边AD的中点,BE⊥EC,BE=4,CE=3,求?ABCD的周长和面积.
如图,点E是?ABCD边AD的中点,BE⊥EC,BE=4,CE=3,求?ABCD的周长和面积.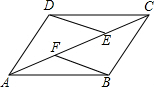 已知如图在平行四边形ABCD中,E、F是对角线AC上的两点,且AE=CF,求证:∠AED=∠CFB.
已知如图在平行四边形ABCD中,E、F是对角线AC上的两点,且AE=CF,求证:∠AED=∠CFB.