题目内容
6.己知:在四边形ABCD中,G、H分别是AD、BC的中点,AE⊥BD,CF⊥BD,垂足分别为E、F.(1)如图1,若四边形ABCD为平行四边形,求证:四边形GEHF是平行四边形.
(2)如图2,若四边形ABCD为矩形,设$\frac{AD}{AB}$=n.请你给出一个n的值,使四边形GEHF为矩形,并说明理由.
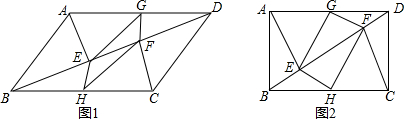
分析 (1)根据直角三角形斜边中线定理只要证明EG=HF,EG∥FH即可.
(2)结论n=$\sqrt{3}$,如图2中,连接GH,交BD于O,连接AO,先证明△ABO是等边三角形,再证明AB=EF,GH=AB,得EF=HG,即可证明.
解答 (1)证明:如图1中,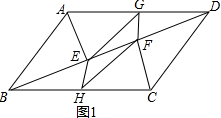 ∵AE⊥BD,CF⊥BD,
∵AE⊥BD,CF⊥BD,
∴∠AED=∠CFB=90°,
∵AG=GD,BH=CH,
∴EG=$\frac{1}{2}$AD,HF=$\frac{1}{2}$BC,
∴∠GDE=∠GED,∠HBF=∠HFB,
∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∴∠GDE=∠HBF,
∴EG=FH,∠GEF=∠HFE,
∴EG∥HF,
∴四边形GEHF是平行四边形.
(2)当n=$\sqrt{3}$时,四边形GEHF为矩形.
证明:如图2中,连接GH,交BD于O,连接AO.
由(1)可知,四边形GEHF是平行四边形,
∴OE=OF,
∵四边形ABCD是矩形,
∴∠BAD=90°,
∵tan∠ABD=$\frac{AD}{AB}$=$\sqrt{3}$,
∴∠ABD=60°,∠ADB=30°,
∵AE⊥BD,
∴∠AED=90°,∠EAD=60°,∠BAE=30°,
∴BE=$\frac{1}{2}$AB,同理DF=$\frac{1}{2}$CD,
∵AB=CD,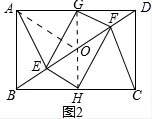
∴BE=DF,BO=OD,
∴AO=BO=DO,
∵∠ABD=60°,
∴△ABO是等边三角形,
∴AB=AO,∵AE⊥BO,
∴BE=EO,
∴EF=2BE=AB,
∵AG∥BH,AG=BH,
∴四边形ABHG是平行四边形,
∴AB=GH=EF,∵四边形GEHF是平行四边形,
∴四边形GEHF是矩形.
点评 本题考查平行四边形的判定和性质、矩形的判定和性质、直角三角形斜边中线定理、等边三角形的判定等知识,灵活运用这些知识是解决问题的关键,属于中考常考题型.

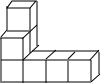 如图,是由相同小正方形组成的立方体图形,它的左视图为( )
如图,是由相同小正方形组成的立方体图形,它的左视图为( )| A. | 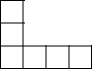 | B. | 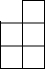 | C. | 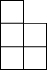 | D. |  |
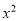
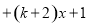 =0,
=0,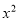

 =0.
=0. 的值.
的值.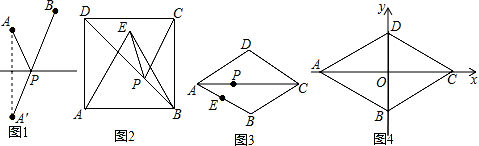
 如图,已知△ABC和点O,画出△DEF和△ABC关于点P成中心对称.
如图,已知△ABC和点O,画出△DEF和△ABC关于点P成中心对称.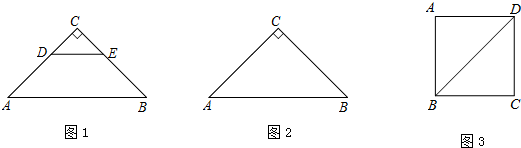
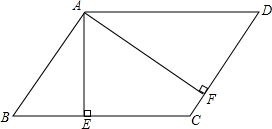 如图.在平行四边形ABCD中,AE⊥BC,AF⊥CD,垂足分别为点E,F.该图中与∠EAF相等的有∠B、∠D.
如图.在平行四边形ABCD中,AE⊥BC,AF⊥CD,垂足分别为点E,F.该图中与∠EAF相等的有∠B、∠D.