题目内容
3.若a>b,则下列不等式中错误的是( )| A. | 4-3a>4-3b | B. | $\frac{a}{2}$>$\frac{b}{2}$ | C. | 3a-4>3b-4 | D. | a+1>b+1 |
分析 根据不等式的性质逐个判断即可.
解答 解:A、∵a>b,
∴-3a<-3b,
∴4-3a<4-3b,故本选项符合题意;
B、∵a>b,
∴$\frac{a}{2}$>$\frac{b}{2}$,故本选项不符合题意;
C、∵a>b,
∴3a>3b,
∴3a-4>3b-4,故本选项不符合题意;
D、∵a>b,
∴a+1>b+1,故本选项不符合题意;
故选A.
点评 本题考查了不等式的性质,能正确根据不等式的性质进行变形是解此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.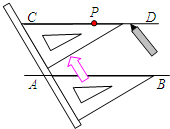 如图,给出了过直线AB外一点P,作已知直线AB的平行线的方法,其依据是( )
如图,给出了过直线AB外一点P,作已知直线AB的平行线的方法,其依据是( )
 如图,给出了过直线AB外一点P,作已知直线AB的平行线的方法,其依据是( )
如图,给出了过直线AB外一点P,作已知直线AB的平行线的方法,其依据是( )| A. | 同位角相等,两直线平行 | |
| B. | 内错角相等,两直线平行 | |
| C. | 同旁内角互补,两直线品行 | |
| D. | 过直线外一点有且只有一条直线与这条直线平行 |
8.与$\sqrt{2}$是同类二次根式的是( )
| A. | $\sqrt{2}$ | B. | $\sqrt{\frac{1}{8}}$ | C. | $\sqrt{0.2}$ | D. | $\sqrt{27}$ |
15.下列调查中适合采用普查的是( )
| A. | 调查市场上某种白酒中塑化剂的含量 | |
| B. | 调查鞋厂生产的鞋底能承受的弯折次数 | |
| C. | 了解某火车的一节车厢内感染禽流感病毒的人数 | |
| D. | 了解某城市居民收看江苏卫视的时间 |
12.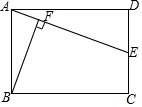 如图,在矩形ABCD中,AB=2,BC=3.若点E是边CD的中点,连接AE,过点B作BF⊥AE交AE于点F,则BF的长为( )
如图,在矩形ABCD中,AB=2,BC=3.若点E是边CD的中点,连接AE,过点B作BF⊥AE交AE于点F,则BF的长为( )
 如图,在矩形ABCD中,AB=2,BC=3.若点E是边CD的中点,连接AE,过点B作BF⊥AE交AE于点F,则BF的长为( )
如图,在矩形ABCD中,AB=2,BC=3.若点E是边CD的中点,连接AE,过点B作BF⊥AE交AE于点F,则BF的长为( )| A. | $\frac{3\sqrt{10}}{2}$ | B. | $\frac{3\sqrt{10}}{5}$ | C. | $\frac{\sqrt{10}}{5}$ | D. | $\frac{3\sqrt{5}}{5}$ |
8.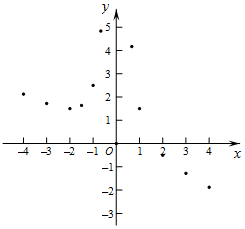 有这样一个问题:探究函数y=$\frac{2}{{x}^{2}}$-$\frac{1}{2}$x的图象与性质.
有这样一个问题:探究函数y=$\frac{2}{{x}^{2}}$-$\frac{1}{2}$x的图象与性质.
小东根据学习函数的经验,对函数y=$\frac{2}{{x}^{2}}$-$\frac{1}{2}$x的图象与性质进行了探究.
下面是小东的探究过程,请补充完整,并解决相关问题:
(1)函数y=$\frac{2}{{x}^{2}}$-$\frac{1}{2}$x的自变量x的取值范围是x≠0;
(2)下表是y与x的几组对应值,求m的值;
(3)如图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;
(4)进一步探究发现,该函数图象在第二象限内的最低点的坐标是(-2,$\frac{3}{2}$),结合函数的图象,写出该函数的其它性质(一条即可)当x>0时,y随x的增大而减小.
(5)根据函数图象估算方程$\frac{2}{{x}^{2}}$-$\frac{1}{2}$x=2的根为x1=-3.8,x2=-1.8.(精确到0.1)
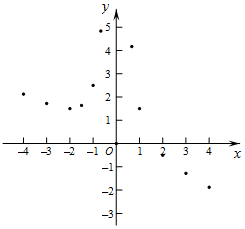 有这样一个问题:探究函数y=$\frac{2}{{x}^{2}}$-$\frac{1}{2}$x的图象与性质.
有这样一个问题:探究函数y=$\frac{2}{{x}^{2}}$-$\frac{1}{2}$x的图象与性质.小东根据学习函数的经验,对函数y=$\frac{2}{{x}^{2}}$-$\frac{1}{2}$x的图象与性质进行了探究.
下面是小东的探究过程,请补充完整,并解决相关问题:
(1)函数y=$\frac{2}{{x}^{2}}$-$\frac{1}{2}$x的自变量x的取值范围是x≠0;
(2)下表是y与x的几组对应值,求m的值;
| x | … | -4 | -3 | -2 | -$\frac{3}{2}$ | -1 | -$\frac{2}{3}$ | $\frac{2}{3}$ | 1 | 2 | 3 | 4 | … |
| y | … | $\frac{17}{8}$ | $\frac{31}{18}$ | $\frac{3}{2}$ | $\frac{59}{36}$ | $\frac{5}{2}$ | $\frac{29}{6}$ | $\frac{25}{6}$ | $\frac{3}{2}$ | -$\frac{1}{2}$ | -$\frac{23}{18}$ | m | … |
(4)进一步探究发现,该函数图象在第二象限内的最低点的坐标是(-2,$\frac{3}{2}$),结合函数的图象,写出该函数的其它性质(一条即可)当x>0时,y随x的增大而减小.
(5)根据函数图象估算方程$\frac{2}{{x}^{2}}$-$\frac{1}{2}$x=2的根为x1=-3.8,x2=-1.8.(精确到0.1)
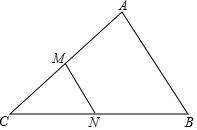 如图,在△ABC中,M、N分别为AC,BC的中点.若S△CMN=1,则S四边形ABNM=3.
如图,在△ABC中,M、N分别为AC,BC的中点.若S△CMN=1,则S四边形ABNM=3.