题目内容
11．
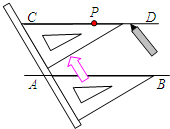如图，给出了过直线AB外一点P，作已知直线AB的平行线的方法，其依据是（ ）| A． | 同位角相等，两直线平行 | |
| B． | 内错角相等，两直线平行 | |
| C． | 同旁内角互补，两直线品行 | |
| D． | 过直线外一点有且只有一条直线与这条直线平行 |
分析 过直线外一点作已知直线的平行线，只有满足同位角相等，才能得到两直线平行．
解答 解：由图形得，有两个相等的同位角，所以只能依据：同位角相等，两直线平行．
故选A．
点评 本题考查的是作图-复杂作图，熟知过直线外一点，作已知直线的平行线的方法是解答此题的关键．
练习册系列答案
相关题目
1．以下是关于正多边形的描述：
①正多边形的每条边都相等； ②正多边形都是轴对称图形；
③正多边形的外角和是360°；④正多边形都是中心对称图形．
其中正确的描述是（ ）
①正多边形的每条边都相等； ②正多边形都是轴对称图形；
③正多边形的外角和是360°；④正多边形都是中心对称图形．
其中正确的描述是（ ）
| A． | ①②③ | B． | ①②④ | C． | ②③④ | D． | ①②③④ |
星期日，小英与小平同时从家里出发返回学校，速度分别为3千米/小时，4千米/小时，小平家离学校18千米，小英家在小平返校的路上，离小平家2千米．
6．下列计算结果正确的是（ ）
| A． | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | B． | 2$\sqrt{3}$-$\sqrt{3}$=2 | C． | $\sqrt{2}$×$\sqrt{3}$=$\sqrt{6}$ | D． | $\frac{\sqrt{2}}{\sqrt{5}}$=5$\sqrt{10}$ |
16．
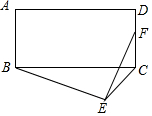如图，在矩形ABCD中，AB=5，AD=12，以BC为斜边在矩形外部作直角三角形BEC，F为CD的中点，则EF的最大值为（ ）
如图，在矩形ABCD中，AB=5，AD=12，以BC为斜边在矩形外部作直角三角形BEC，F为CD的中点，则EF的最大值为（ ）| A． | $\frac{\sqrt{433}}{2}$ | B． | $\frac{25}{4}$ | C． | $\frac{25}{2}$ | D． | $\frac{\sqrt{433}}{4}$ |
3．若a＞b，则下列不等式中错误的是（ ）
| A． | 4-3a＞4-3b | B． | $\frac{a}{2}$＞$\frac{b}{2}$ | C． | 3a-4＞3b-4 | D． | a+1＞b+1 |