题目内容
8．与$\sqrt{2}$是同类二次根式的是（ ）| A． | $\sqrt{2}$ | B． | $\sqrt{\frac{1}{8}}$ | C． | $\sqrt{0.2}$ | D． | $\sqrt{27}$ |
分析 根据同类二次根式是化为最简二次根式后，被开方数相同的二次根式称为同类二次根式，可得答案．
解答 解：A.$\sqrt{2}$=$\sqrt{2}$，不是同类二次根式；故本选项错误；
B.$\sqrt{\frac{1}{8}}$=$\frac{\sqrt{2}}{4}$，与，$\sqrt{2}$是同类二次根式，故本选项正确；
C.$\sqrt{0.2}$=$\frac{\sqrt{5}}{5}$，与$\sqrt{2}$不是同类二次式，故本选项错误；
D.$\sqrt{27}$=$3\sqrt{3}$，与$\sqrt{2}$不是同类二次式，故本选项错误；
故选B．
点评 本题考查了同类二次根式的定义，把二次根式化为最简二次根式是解题的关键．
练习册系列答案
名校课堂系列答案
相关题目
16．
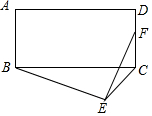如图，在矩形ABCD中，AB=5，AD=12，以BC为斜边在矩形外部作直角三角形BEC，F为CD的中点，则EF的最大值为（ ）
如图，在矩形ABCD中，AB=5，AD=12，以BC为斜边在矩形外部作直角三角形BEC，F为CD的中点，则EF的最大值为（ ）| A． | $\frac{\sqrt{433}}{2}$ | B． | $\frac{25}{4}$ | C． | $\frac{25}{2}$ | D． | $\frac{\sqrt{433}}{4}$ |
3．若a＞b，则下列不等式中错误的是（ ）
| A． | 4-3a＞4-3b | B． | $\frac{a}{2}$＞$\frac{b}{2}$ | C． | 3a-4＞3b-4 | D． | a+1＞b+1 |
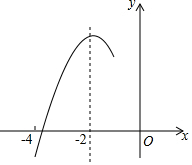如图，抛物线y=ax2+bx+c（a≠0）的对称轴为直线x=-2，与x轴的一个交点在（-3，0）和（-4，0）之间，其部分图象如图所示．则下列结论：①4a-b=0；②c＜0；③-3a+c＞0；④4a-2b＞at2+bt（t为实数）；⑤点（-$\frac{9}{2}$，y1），（-$\frac{5}{2}$，y2），（-$\frac{1}{2}$，y3）是该抛物线上的点，则y1＜y2＜y3，正确的个数有（ ）
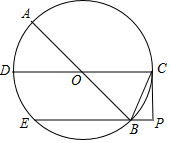如图，AB、CD是⊙O的直径，BE是⊙O的弦，且BE∥CD，过点C的切线与EB的延长线交于点P，连接BC．