题目内容
抛物线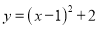
的顶点坐标是（ ）
A. （-1，2） B. （-1，-2） C. （1，2） D. （1，-2）
C
【解析】利用抛物线顶点式的特点直接写出顶点坐标是（h，k），可知抛物线y=（x-1）2+2的顶点坐标是（1，2）．
故选：C．
练习册系列答案
相关题目
若y＝(m2－3m)x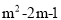
是二次函数，则m＝____．
-1
【解析】由二次函数的定义可知自变量的最高指数为2，且系数不等于0，可得m2－3m≠0，且；解得m=-1或m=3；当m=3时，m2－3m=0；最终可求得m=-1．
故答案为：-1. 下列各式从左到右的变形（1）15x2y=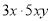
；（2）(x+y)(x-y)=x2-y2；
（3）x2-6x+9=(x-3)2；（4）x2+4x+1=x(x+4+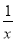
)，其中是因式分解的个数是（ ）
A. 1个 B. 2个 C. 3个 D. 4个
A
【解析】把一个多项式化成几个整式的积的形式，叫做把这个多项式分解因式.根据因式分解的定义可得只有（3）符合要求，故选A. 二次函数y＝x ²－x＋m(m为常数)的图象如图所示，当x＝a时，y＜0；那么当x＝a－1时，函数值（ ）
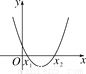
A. y＜0 B. 0＜y＜m C. y＞m D. y＝m
C
【解析】试题分析：根据对称轴及函数值判断a的取值范围，从而得出a﹣1＜0，因为当x是y随x的增大而减小，所以当x=a﹣1＜0时，函数值y一定大于m．
【解析】
当x=a时，y＜0，
则a的范围是x1＜a＜x2，
又对称轴是x=，
所以a﹣1＜0，
当x是y随x的增大而减小，
当x=0是函数值是m．
因而当x=a﹣1＜0时，函数值y一定大于m．
... 如图图形中，阴影部分面积相等的是（ ）
A. 甲 乙
B. 甲 丙
C. 乙 丙
D. 丙 丁
B
【解析】根据题意，可知：
甲：直线与x轴交点为（3，0），与y轴的交点为（0，4），则阴影部分的面积为×3×4=6；
乙：阴影部分为斜边为4的等腰直角三角形，其面积为×4×2=4；
丙：抛物线与x轴的两个交点为（-3，0）与（3，0），顶点坐标为（0，-2），则阴影部分的面积为×6×2=6；
丁：此函数是反比例函数，那么阴影部分的面积为×6=3；
因此甲、丙... 设抛物线y=ax2+bx+c(a≠0)过点A(0，2)，B(4，3)，C三点，其中点C在直线x=2上，且点C到抛物线的对称轴的距离等于1，则抛物线的函数解析式为______.
y=x2-x+2或y=-x2+x+2.
【解析】试题分析：∵抛物线过A(0，2)，∴.
∵抛物线过B(4，3)，∴.
∵抛物线过C，且点C在直线上，点C到抛物线对称轴的距离等于1，
∴.
∴或，解得或.
∴抛物线的函数解析式为或. 二次函数y=-x2+bx+c的图象的最高点是(-1，-3)，则b，c的值分别是( )
A. b=2，c=4 B. b=2，c=-4 C. b=-2，c=4 D. b=-2，c=-4
D
【解析】试题分析：由题可得函数顶点坐标是（-1，-3）所以对称轴是x=-1,对称轴x=,a=-1,所以b=-2,将点（-1，-3）代入表达式得c=-4,所以函数表达式为y=-x2-2x-4,故b=-2,c=-4,故选D. 一个二次函数的图象经过点A（0，0），B（-1，-11），C（1，9）三点，则这个二次函数的关系式是（ ）
A.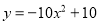 
B.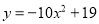 
C.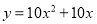 
D.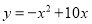 
D
【解析】由于抛物线经过原点，则可以设其函数关系式为，
将B、C两点坐标代入，得
解得
则函数关系式为
故选：D． 将抛物线y=x2向左平移4个单位后，再向下平移2个单位，则此时抛物线的解析式是________．
y=（x+4）2-2
【解析】∵y=x2向左平移4个单位后,再向下平移2个单位. ∴y= .故此时抛物线的解析式是y=.故答案为：y=（x+4）2-2.