题目内容
将抛物线y=x2向左平移4个单位后,再向下平移2个单位,则此时抛物线的解析式是________.
 y=(x+4)2-2
【解析】∵y=x2向左平移4个单位后,再向下平移2个单位. ∴y= .故此时抛物线的解析式是y=.故答案为:y=(x+4)2-2.
y=(x+4)2-2
【解析】∵y=x2向左平移4个单位后,再向下平移2个单位. ∴y= .故此时抛物线的解析式是y=.故答案为:y=(x+4)2-2.
练习册系列答案
相关题目
抛物线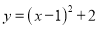 的顶点坐标是( )
的顶点坐标是( )
A. (-1,2) B. (-1,-2) C. (1,2) D. (1,-2)
 C
【解析】利用抛物线顶点式的特点直接写出顶点坐标是(h,k),可知抛物线y=(x-1)2+2的顶点坐标是(1,2).
故选:C.
C
【解析】利用抛物线顶点式的特点直接写出顶点坐标是(h,k),可知抛物线y=(x-1)2+2的顶点坐标是(1,2).
故选:C. 当m=_______时,关于x的方程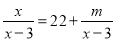 有增根.
有增根.
 3
【解析】去分母,两边同时乘以x-3,得
x=22(x-3)+m,
∵方程产生增根,
∴x-3=0,
∴x=3,
代入整式方程得,3=m,
解得m=3,
∴当m=3时,原方程会产生增根,
故答案为:3.
3
【解析】去分母,两边同时乘以x-3,得
x=22(x-3)+m,
∵方程产生增根,
∴x-3=0,
∴x=3,
代入整式方程得,3=m,
解得m=3,
∴当m=3时,原方程会产生增根,
故答案为:3. 某煤矿原计划x天生存120t煤,由于采用新的技术,每天增加生存3t,因此提前2天完成,列出的方程为( )
A. 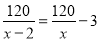 B.
B. 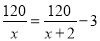
C. 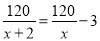 D.
D. 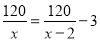
 D
【解析】因为原计划x天生产120吨煤,所以原计划每天生产吨,因为采取新的技术,提前2天 ,所以现在每天生产吨,因为现在每天比原计划每天增加3吨,所以可列方程是,故选D.
D
【解析】因为原计划x天生产120吨煤,所以原计划每天生产吨,因为采取新的技术,提前2天 ,所以现在每天生产吨,因为现在每天比原计划每天增加3吨,所以可列方程是,故选D. 用配方法把二次函数y=l+2x-x2化为y=a(x-h)2+k的形式,作出它的草图,回答下列问题.
(1)求抛物线的顶点坐标和它与x轴的交点坐标;
(2)当x取何值时,y随x的增大而增大?
(3)当x取何值时,y的值大于0?
 y=-(x-1)2+2(1)顶点坐标为(1,2),与x轴的两个交点坐标分别为(1-,0),(1+,0)(2)当x<1时,y随x的增大而增大.(3)当l-<x<1+时,y的值大于0
【解析】分析:(1)利用配方法得到y=-(x-1)²+2,则根据二次函数的性质可得到抛物线的顶点坐标;再利用抛物线与x轴的交点问题,通过解方程-(x-1)²+2=0可得到它与x轴的交点坐标;(2)根据二次函数的性质...
y=-(x-1)2+2(1)顶点坐标为(1,2),与x轴的两个交点坐标分别为(1-,0),(1+,0)(2)当x<1时,y随x的增大而增大.(3)当l-<x<1+时,y的值大于0
【解析】分析:(1)利用配方法得到y=-(x-1)²+2,则根据二次函数的性质可得到抛物线的顶点坐标;再利用抛物线与x轴的交点问题,通过解方程-(x-1)²+2=0可得到它与x轴的交点坐标;(2)根据二次函数的性质... 已知抛物线过A(-1,0),B(3,0)两点,与y轴交于C点,且BC=3 ,则这条抛物线的解析式为 ( )
,则这条抛物线的解析式为 ( )
A. y=-x2+2x+3 B. y=x2-2x-3
C. y=x2+2x―3或y=-x2+2x+3 D. y=-x2+2x+3或y=x2-2x-3
 D
【解析】∵A、B两点的纵坐标为0.
∴A、B为抛物线与x轴的交点,
∴△OBC为直角三角形。
又∵C点有可能在y轴的负半轴,也可能在y轴的正半轴。
∴C点的纵坐标为3或?3(根据勾股定理求得).
∴C点的纵坐标为(0,3)或(0,?3).
设函数的解析式为y=ax²+bx+c,
(1)则当抛物线经过(?1,0)、(3,0)、(0,?3)三点时,
...
D
【解析】∵A、B两点的纵坐标为0.
∴A、B为抛物线与x轴的交点,
∴△OBC为直角三角形。
又∵C点有可能在y轴的负半轴,也可能在y轴的正半轴。
∴C点的纵坐标为3或?3(根据勾股定理求得).
∴C点的纵坐标为(0,3)或(0,?3).
设函数的解析式为y=ax²+bx+c,
(1)则当抛物线经过(?1,0)、(3,0)、(0,?3)三点时,
... 如图,有A、B两艘船在大海中航行,B船在A船的正东方向,且两船保持20海里的距离,某一时刻这两艘船同时测得在A的东北方向,B的北偏东15°方向有另一艘船C,那么此时船C与船B的距离是_______海里.(结果保留根号)
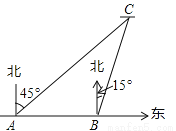
 20
【解析】试题分析:过点B作BD⊥AC,则△ABD为等腰直角三角形,则BD=10海里,在Rt△CBD中,∠CBD=60°,则BC=2BD=20海里.
20
【解析】试题分析:过点B作BD⊥AC,则△ABD为等腰直角三角形,则BD=10海里,在Rt△CBD中,∠CBD=60°,则BC=2BD=20海里. 如图,一艘海轮位于灯塔P的北偏东30°方向,距离灯塔60海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45°方向上的B处,这时,海轮所在的B处与灯塔P的距离为( )
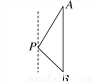
A. 30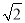 海里 B. 30
海里 B. 30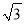 海里 C. 60海里 D. 30
海里 C. 60海里 D. 30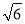 海里
海里
 A
【解析】试题分析:过点P作PC⊥AB于点C. 在Rt△PAC中,∵PA=60海里,∠PAC=30°, ∴CP=AP=30海里.
在Rt△PBC中,∵PC=30海里,∠PBC=∠BPC=45°, ∴PB=PC=30海里.
即海轮所在的B处与灯塔P的距离为30海里.
A
【解析】试题分析:过点P作PC⊥AB于点C. 在Rt△PAC中,∵PA=60海里,∠PAC=30°, ∴CP=AP=30海里.
在Rt△PBC中,∵PC=30海里,∠PBC=∠BPC=45°, ∴PB=PC=30海里.
即海轮所在的B处与灯塔P的距离为30海里. 若一个多边形除了一个内角外,其余各内角之和是2570°,则这个角是( )
A. 90° B. 15° C. 120° D. 130°
 D
【解析】设这个内角度数为x°,边数为n,
则(n-2)×180-x=2570,
180•n=2930+x,
∵n为正整数,
∴n=17,
∴去掉角度数为180°×(17-2)-2570°=130°,
故选D.
D
【解析】设这个内角度数为x°,边数为n,
则(n-2)×180-x=2570,
180•n=2930+x,
∵n为正整数,
∴n=17,
∴去掉角度数为180°×(17-2)-2570°=130°,
故选D. 
