题目内容
二次函数y=-x2+bx+c的图象的最高点是(-1，-3)，则b，c的值分别是( )
A. b=2，c=4 B. b=2，c=-4 C. b=-2，c=4 D. b=-2，c=-4
D
【解析】试题分析：由题可得函数顶点坐标是（-1，-3）所以对称轴是x=-1,对称轴x=,a=-1,所以b=-2,将点（-1，-3）代入表达式得c=-4,所以函数表达式为y=-x2-2x-4,故b=-2,c=-4,故选D.
练习册系列答案
开心快乐假期作业暑假作业西安出版社系列答案
名题训练系列答案
期末集结号系列答案
相关题目
观察下列各式：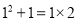 
； 
； 
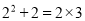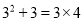；……，请你将猜想到的规律用自然数
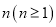的式子表示出来_________.
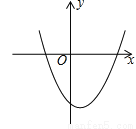
【解析】观察所给的式子，根据所给式子揭示的规律，即可得一般的规律： . 已知二次函数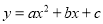
的图象如图所示，则点P（a，bc）在第_______象限．
一
【解析】从图象得出，二次函数的对称轴在y轴的右侧，且开口向上，可得a＞0， ＞0，所以b＜0，然后由二次函数的图象与y轴交于y轴的负半轴，得c＜0，即可得到a＞0，bc＞0，则点P（a，bc）在第一象限．
故答案为：一． 抛物线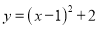
的顶点坐标是（ ）
A. （-1，2） B. （-1，-2） C. （1，2） D. （1，-2）
C
【解析】利用抛物线顶点式的特点直接写出顶点坐标是（h，k），可知抛物线y=（x-1）2+2的顶点坐标是（1，2）．
故选：C． 将二次函数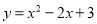
化为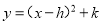
的形式，结果为（ ）
A.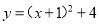 
B.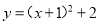 
C. 
D. 
D
【解析】
故选：D． 已知抛物线的顶点坐标为M（1，﹣2），且经过点N（2，3），求此二次函数的解析式．
y=5（x﹣1）2﹣2
【解析】试题分析：因为已知顶点坐标，所以可设抛物线顶点式： ，仅有一待定系数a，故只需找出图象上一个已知点，代入即可得到一个关于a的一元一次方程，解之，得a值，即可得到所求解析式.
【解析】
∵抛物线的顶点坐标为M（1，﹣2），
∴设此二次函数的解析式为y=a（x﹣1）2﹣2，
把点（2，3）代入解析式，得：
，
解得 a =5，
... 用配方法将y=-2x2+4x+6化成y=a（x+h）2+k的形式，则a+h+k的值为（ ）
A. 5
B. 7
C. -1
D. -2
A
【解析】
∴a=-2，h=-1，k=8
∴a+h+k=-2+（-1）+8=5
故选：A． 当m＝_______时，关于x的方程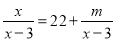
有增根．
3
【解析】去分母，两边同时乘以x-3，得
x=22(x-3)+m，
∵方程产生增根，
∴x-3=0，
∴x=3，
代入整式方程得，3=m，
解得m=3，
∴当m=3时，原方程会产生增根，
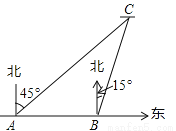
故答案为：3. 如图，有A、B两艘船在大海中航行，B船在A船的正东方向，且两船保持20海里的距离，某一时刻这两艘船同时测得在A的东北方向，B的北偏东15°方向有另一艘船C，那么此时船C与船B的距离是_______海里．（结果保留根号）
20
【解析】试题分析：过点B作BD⊥AC，则△ABD为等腰直角三角形，则BD=10海里，在Rt△CBD中，∠CBD=60°，则BC=2BD=20海里．