题目内容
设抛物线y=ax2+bx+c(a≠0)过点A(0，2)，B(4，3)，C三点，其中点C在直线x=2上，且点C到抛物线的对称轴的距离等于1，则抛物线的函数解析式为______.
y=x2-x+2或y=-x2+x+2.
【解析】试题分析：∵抛物线过A(0，2)，∴.
∵抛物线过B(4，3)，∴.
∵抛物线过C，且点C在直线上，点C到抛物线对称轴的距离等于1，
∴.
∴或，解得或.
∴抛物线的函数解析式为或.
对于抛物线y＝ax2，下列说法中正确的是（ ）
A. a越大，抛物线开口越大
B. a越小，抛物线开口越大
C. ｜a｜越大，抛物线开口越大
D. ｜a｜越小，抛物线开口越大
D
【解析】试题分析：∵对于y＝ax2图像而言，|a|越小，开口越大
∴D是正确的 如果二次函数的二次项系数为l，则此二次函数可表示为y=x2+px+q，我们称[p，q]为此函数的特征数，如函数y=x2+2x+3的特征数是[2，3]．
（1）若一个函数的特征数为[﹣2，1]，求此函数图象的顶点坐标．
（2）探究下列问题：
①若一个函数的特征数为[2，﹣1]，将此函数的图象先向右平移1个单位，再向上平移1个单位，求得到的图象对应的函数的特征数．
②若一个函数的特征数为[4，2]，问此函数的图象经过怎样的平移，才能使得到的图象对应的函数的特征数为[2，4]？
（1）此函数图象的顶点坐标为：（1，0）；（2）图象对应的函数的特征数为：[0，﹣1]；（3）原函数的图象向右平移1个单位，再向上平移5个单位得到．
【解析】试题分析：（1）根据特征数的定义，得二次函数为y=x2﹣2x+1，再利用配方得：y=（x﹣1）2，从而顶点坐标为（1,0）
（2）①根据特征数的定义，得二次函数为y=x2+2x-1，再利用配方得y=（x+1）2﹣2，图象先向右平移... 已知抛物线y=ax2+bx+c开口向下，顶点坐标（3，-5），那么该抛物线有（ ）
A. 最小值-5
B. 最大值-5
C. 最小值3
D. 最大值3
B
【解析】由抛物线的开口向下和其顶点坐标为（3，-5），根据抛物线的性质，可以知该抛物线有最大值-5．
故选：B． 抛物线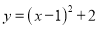
的顶点坐标是（ ）
A. （-1，2） B. （-1，-2） C. （1，2） D. （1，-2）
C
【解析】利用抛物线顶点式的特点直接写出顶点坐标是（h，k），可知抛物线y=（x-1）2+2的顶点坐标是（1，2）．
故选：C． 若y＝ax2＋bx＋c，则由表格中信息可知y与x之间的函数表达式是( )
x | －1 | 0 | 1 |
ax2 | 1 | ||
ax2＋bx＋c | 8 | 3 |
A. y＝x2－4x＋3 B. y＝x2－3x＋4
C. y＝x2－3x＋3 D. y＝x2－4x＋8
A
【解析】把表格中所给的的三对对应值代入对应的式子可得： ，解得： ，
∴与之间的函数表达式为：.
故选A. 已知抛物线的顶点坐标为M（1，﹣2），且经过点N（2，3），求此二次函数的解析式．
y=5（x﹣1）2﹣2
【解析】试题分析：因为已知顶点坐标，所以可设抛物线顶点式： ，仅有一待定系数a，故只需找出图象上一个已知点，代入即可得到一个关于a的一元一次方程，解之，得a值，即可得到所求解析式.
【解析】
∵抛物线的顶点坐标为M（1，﹣2），
∴设此二次函数的解析式为y=a（x﹣1）2﹣2，
把点（2，3）代入解析式，得：
，
解得 a =5，
... 若所求的二次函数图象与抛物线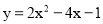
有相同的顶点，并且在对称轴的左侧，y随x的增大而增大，在对称轴的右侧，y随x的增大而减小，则所求二次函数的解析式为（ ）
A.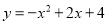 
B.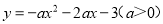 
C.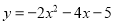 
D.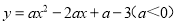 
D
【解析】抛物线y=2x2-4x-1的顶点坐标为（1，-3），根据题意得所求的二次函数的解析式的顶点坐标是（1，-3），且抛物线开口向下．
A．抛物线开口向下，顶点坐标是（1，5），所以选项错误；
B．抛物线开口向下，顶点坐标是（1，-3a-3），所以选项错误；
C．抛物线开口向下，顶点坐标是（-1，-3），所以选项错误；
D．抛物线开口向下，顶点坐标是（1，-3）... 已知抛物线过A(－1，0)，B(3，0)两点，与y轴交于C点，且BC=3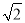
，则这条抛物线的解析式为 ( )
A. y=－x2+2x+3 B. y＝x2－2x－3
C. y=x2+2x―3或y＝－x2+2x+3 D. y=－x2+2x+3或y＝x2－2x－3
D
【解析】∵A、B两点的纵坐标为0.
∴A、B为抛物线与x轴的交点，
∴△OBC为直角三角形。
又∵C点有可能在y轴的负半轴，也可能在y轴的正半轴。
∴C点的纵坐标为3或?3(根据勾股定理求得).
∴C点的纵坐标为(0,3)或(0,?3).
设函数的解析式为y=ax²+bx+c，
(1)则当抛物线经过(?1,0)、(3,0)、(0,?3)三点时，
...