题目内容
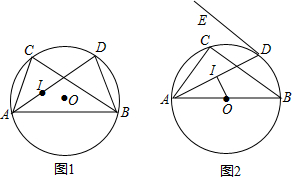
19．
如图，∠1=∠E，∠2与∠C互余，DB垂直平分AC，垂足为点F，请说明AC平分DB．
分析 只要证明△DFC≌△BFA即可解决问题．
解答 解：∵∠1=∠E，
∴AE∥BD，
∴∠B=∠2，
∵BD垂直平分AC，
∴∠DFC=90°，
∴∠1+∠C=90°，∵∠2+∠C=90°，
∴∠1=∠2，
∴∠B=∠1，
∵∠DFC=∠BFA，AF=CF，
∴△DFC≌△BFA，
∴DF=BF，
∴AC平分DB．
点评 本题考查平行线的判定、线段的垂直平分线的定义、全等三角形的判定和性质等知识，解题的关键是灵活运用所学知识解决问题，属于中考常考题型．
练习册系列答案
相关题目
10．
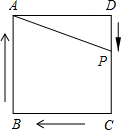如图，正方形ABCD的边长为4，P为正方形边上一动点，运动路线是D→C→B→A，设P点经过的路程为x，以点A、P、D为顶点的三角形的面积是y，则下列图象能大致反映y与x的函数关系的是（ ）
如图，正方形ABCD的边长为4，P为正方形边上一动点，运动路线是D→C→B→A，设P点经过的路程为x，以点A、P、D为顶点的三角形的面积是y，则下列图象能大致反映y与x的函数关系的是（ ）| A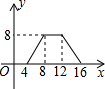． |  | B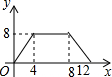． |  | C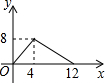． |  | D． |  |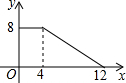
7．
如图，∠ACB=90°，CD⊥AB于D，下列结论错误的是（ ）
如图，∠ACB=90°，CD⊥AB于D，下列结论错误的是（ ）| A． | ∠1=∠B | B． | ∠2=∠1 | ||
| C． | ∠2和∠A都是∠B的余角 | D． | AC•BC=AB•CD |
14．定义：a是不为1的有理数，我们把$\frac{1}{1-a}$称为a的差倒数，如：2的差倒数是$\frac{1}{1-2}$=-1，-1的差倒数是$\frac{1}{1-（-1）}$=$\frac{1}{2}$，已知a1=-$\frac{1}{3}$，a2是a1的差倒数，a1是a2的差倒数，a4是a3的差倒数，…，以此类推，a2009的值为（ ）
| A． | -$\frac{1}{3}$ | B． | $\frac{3}{4}$ | C． | 4 | D． | $\frac{4}{3}$ |
4．下列推理中，以“等量代换”为推理数据的是（ ）
| A． | ∵∠1=∠2，∠2=∠3，∴∠1=∠3 | B． | ∵a∥b，b∥c，∴a∥c | ||
| C． | ∵∠1=∠2，∴$\frac{1}{2}$∠1=$\frac{1}{2}$∠2 | D． | ∵∠1+∠2=90°，∠1+∠3=90°，∴∠2=∠3 |
如图，OC⊥OD，∠1=50°，则∠2的度数是40°．