Question

8．已知I是△ABC的内心，AI延长线交△ABC外接圆于D，连BD．
（1）在图1中，求证：DB=DI；
（2）如图2，若AB为直径，且OI⊥AD于I点，DE切圆于D点，求sin∠ADE的值．

Answer 1

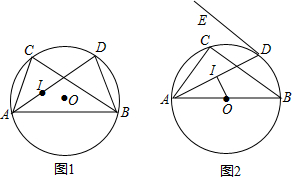
分析 （1）连接BI，由I是△ABC的内心，得到AD平分∠CAB，BI平分∠ABC，根据角平分线的定义得到∠CAD=∠BAD，∠ABI=∠CBI，得到∠DAB=∠CBD，根据三角形的外角的性质得到∠DIB=∠DBI，于是得到BD=DI；
（2）连接BD，根据AB为直径，得到∠ADB=90°，根据垂径定理得到AD=2DI，根据勾股定理得到AB=$\sqrt{A{D}^{2}+B{D}^{2}}$=$\sqrt{5}$BD，根据弦切角定理得到∠ABD=∠ADE，于是得到结论．

解答 解：（1）连接BI，
∵I是△ABC的内心，
∴AD平分∠CAB，BI平分∠ABC，
∴∠CAD=∠BAD，∠ABI=∠CBI，
∵∠CAD=∠DBC，
∴∠DAB=∠CBD，
∵∠DBI=∠DBC+∠CBI，
∠DIB=∠DAB+∠IBA，
∴∠DIB=∠DBI，
∴BD=DI；
（2）连接BD，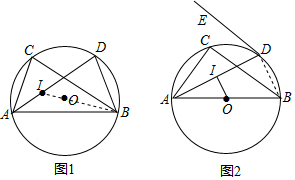
∵AB为直径，
∴∠ADB=90°，
∵OI⊥AD，
∴AD=2DI，
∵BD=DI，
∴AD=2BD，
∴AB=$\sqrt{A{D}^{2}+B{D}^{2}}$=$\sqrt{5}$BD，
∵DE切圆于D点，
∴∠ABD=∠ADE，
∴sin∠ADE=sin∠ABD=$\frac{AD}{AB}$=$\frac{2\sqrt{5}}{5}$．

点评 本题考查了三角形的内切圆与内心，圆周角定理，解直角三角形，正确的作出辅助线是解题的关键．