题目内容
14.定义:a是不为1的有理数,我们把$\frac{1}{1-a}$称为a的差倒数,如:2的差倒数是$\frac{1}{1-2}$=-1,-1的差倒数是$\frac{1}{1-(-1)}$=$\frac{1}{2}$,已知a1=-$\frac{1}{3}$,a2是a1的差倒数,a1是a2的差倒数,a4是a3的差倒数,…,以此类推,a2009的值为( )| A. | -$\frac{1}{3}$ | B. | $\frac{3}{4}$ | C. | 4 | D. | $\frac{4}{3}$ |
分析 计算出前面的几个数据即可发现规律,3个数一个轮回,于是a2009=a2.
解答 解:∵a1=-$\frac{1}{3}$,
∴a2=$\frac{1}{1-(-\frac{1}{3})}$=$\frac{3}{4}$,
a3=$\frac{1}{1-\frac{3}{4}}$=4,
a4=$\frac{1}{1-4}$=-$\frac{1}{3}$,
…
∴每3个数为一周期循环,
∵2009÷3=669…2,
∴a2009=a2=$\frac{3}{4}$,
故选:B.
点评 此题考查了数字的变化类,是一道找规律的题目,要求学生通过观察,分析、归纳发现其中的规律,并应用发现的规律解决问题.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目
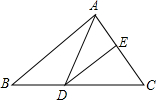 如图,DE是△ABC中AC边的垂直平分线,若AB=7cm,BC=10cm,则△ABD的周长为17cm.
如图,DE是△ABC中AC边的垂直平分线,若AB=7cm,BC=10cm,则△ABD的周长为17cm. 如图,∠AOC和∠BOD都是直角,∠COD=28°,∠AOB=152°.
如图,∠AOC和∠BOD都是直角,∠COD=28°,∠AOB=152°.
 如图,∠1=∠E,∠2与∠C互余,DB垂直平分AC,垂足为点F,请说明AC平分DB.
如图,∠1=∠E,∠2与∠C互余,DB垂直平分AC,垂足为点F,请说明AC平分DB.