题目内容
11.观察下列一组数:列举:3,4,5,猜想:32=4+5;
列举:5,12,13,猜想:52=12+13;
列举:7,24,25,猜想:72=24+25;…
列举:11,b,c,猜想:112=b+c;
请你分析上述数据的规律,结合相关知识求得b=60,c=61.
分析 根据已知条件可找出规律112+b2=c2=(b+1)2;根据此规律可求出b,c的值.
解答 解:由3,4,5知32+42=52=(4+1)2;
由5,12,13知52+122=132=(12+1)2;
由7,24,25知72+242=252=(24+1)2;
故112+b2=c2=(b+1)2;
即132+b2=(b+1)2;
解得b=60,b+1=61,即c=61,
故答案为:60、61.
点评 本题主要考查数字的变化规律,解答此题的关键是根据已知条件可找出规律,利用此规律可求出未知数的值.

练习册系列答案
相关题目
1.下表是某校八年级(1)班43名学生右眼视力的检查结果.
(1)该班学生右眼视力的平均数是4.6(结果保留1位小数).
(2)该班学生右眼视力的中位数是4.7.
(3)该班小鸣同学右眼视力是4.5,能不能说小鸣同学的右眼视力处于全班同学的中上水平?试说明理由.
| 视力 | 4.0 | 4.1 | 4.2 | 4.3 | 4.4 | 4.5 | 4.6 | 4.7 | 4.8 | 4.9 | 5.0 |
| 人数 | 1 | 2 | 5 | 4 | 3 | 5 | 1 | 1 | 5 | 10 | 6 |
(2)该班学生右眼视力的中位数是4.7.
(3)该班小鸣同学右眼视力是4.5,能不能说小鸣同学的右眼视力处于全班同学的中上水平?试说明理由.
 尺规作图(不写作法,保留作图痕迹,写明结论):在数轴上作出表示-$\sqrt{17}$的点.
尺规作图(不写作法,保留作图痕迹,写明结论):在数轴上作出表示-$\sqrt{17}$的点.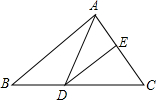 如图,DE是△ABC中AC边的垂直平分线,若AB=7cm,BC=10cm,则△ABD的周长为17cm.
如图,DE是△ABC中AC边的垂直平分线,若AB=7cm,BC=10cm,则△ABD的周长为17cm. 如图,∠AOC和∠BOD都是直角,∠COD=28°,∠AOB=152°.
如图,∠AOC和∠BOD都是直角,∠COD=28°,∠AOB=152°. 如图,∠1=∠E,∠2与∠C互余,DB垂直平分AC,垂足为点F,请说明AC平分DB.
如图,∠1=∠E,∠2与∠C互余,DB垂直平分AC,垂足为点F,请说明AC平分DB.