题目内容
15. 已知:如图,在△ABC中,∠C=∠ABC=2∠A=4∠DBC.求证:BD⊥AC.
已知:如图,在△ABC中,∠C=∠ABC=2∠A=4∠DBC.求证:BD⊥AC.
分析 设∠DBC=x,由题可得∠C=∠ABC=4x,∠A=2x,在△ABC中运用三角形的内角和定理可求出x,然后运用外角的性质可求出∠ADB,即可解决问题.
解答 证明:设∠DBC=x,
∵∠C=∠ABC=2∠A=4∠DBC,
∴∠C=∠ABC=4x,∠A=2x,
∴2x+4x+4x=180°,
∴x=18°,
∴∠C=4×18°=72°,
∴∠ADB=∠DBC+∠C=18°+72°=90°,
∴BD⊥AC.
点评 本题主要考查了三角形的内角和定理、三角形外角的性质、垂直的定义等知识,运用方程思想是解决本题的关键.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
相关题目
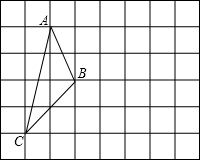 如图,在方格纸中,每个小正方形的边长均为1个单位长度有一个△ABC,它的三个顶点均与小正方形的顶点重合.
如图,在方格纸中,每个小正方形的边长均为1个单位长度有一个△ABC,它的三个顶点均与小正方形的顶点重合.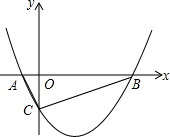 如图,抛物线y=$\frac{1}{2}$x2-$\frac{3}{2}$x-2与x轴相交于点A和点B,与y轴相交于点C,在抛物线上是否存在点P,使得∠PBO=∠BCO?若存在,求出点P的坐标;若不存在,请说明理由.
如图,抛物线y=$\frac{1}{2}$x2-$\frac{3}{2}$x-2与x轴相交于点A和点B,与y轴相交于点C,在抛物线上是否存在点P,使得∠PBO=∠BCO?若存在,求出点P的坐标;若不存在,请说明理由.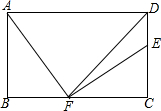 如图,在矩形ABCD中,AD=12,AB=7,DF平分∠ADC,AF⊥EF.
如图,在矩形ABCD中,AD=12,AB=7,DF平分∠ADC,AF⊥EF.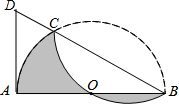 已知,如图,AB是半圆O的直径,点C是$\widehat{AB}$上一点,现将半圆沿BC折叠,$\widehat{BC}$恰好过圆心O,点D为BC延长线上一点,且AD与⊙O相切.
已知,如图,AB是半圆O的直径,点C是$\widehat{AB}$上一点,现将半圆沿BC折叠,$\widehat{BC}$恰好过圆心O,点D为BC延长线上一点,且AD与⊙O相切.