题目内容
20.计算($\frac{5}{a-2}$-a-2)÷$\frac{{a}^{2}-6a+9}{2a-4}$,给a取一个你喜欢的数字代入求值.分析 先把括号内通分和除法运算化为乘法运算,再把分子分母因式分解后约分得到原式=$\frac{-2a-6}{a-3}$,然后把a=0代入计算即可.
解答 解:原式=$\frac{5-(a+2)(a-2)}{a-2}$•$\frac{2(a-2)}{(a-3)^{2}}$
=$\frac{-(a+3)(a-3)}{a-2}$•$\frac{2(a-2)}{(a-3)^{2}}$
=$\frac{-2a-6}{a-3}$,
当a=0时,原式=$\frac{0-6}{0-3}$=2.
点评 本题考查了分式的化简求值:先把分式化简后,再把分式中未知数对应的值代入求出分式的值.在化简的过程中要注意运算顺序和分式的化简.化简的最后结果分子、分母要进行约分,注意运算的结果要化成最简分式或整式.

练习册系列答案
相关题目
3.甲数比乙数的$\frac{1}{4}$还多1,设乙数为x,则甲数可表示为( )
| A. | $\frac{1}{4}x+1$ | B. | 4x-1 | C. | 4(x-1) | D. | 4(x+1) |
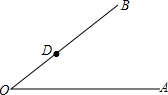 已知,如图,∠A0B边上的点D.过点D作DF∥OA.(保留作图痕迹,不写作法)你有几种方法?
已知,如图,∠A0B边上的点D.过点D作DF∥OA.(保留作图痕迹,不写作法)你有几种方法? 已知:如图,在△ABC中,∠C=∠ABC=2∠A=4∠DBC.求证:BD⊥AC.
已知:如图,在△ABC中,∠C=∠ABC=2∠A=4∠DBC.求证:BD⊥AC.