题目内容
7.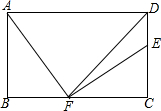 如图,在矩形ABCD中,AD=12,AB=7,DF平分∠ADC,AF⊥EF.
如图,在矩形ABCD中,AD=12,AB=7,DF平分∠ADC,AF⊥EF.(1)求证:AF=EF;
(2)求EF长.
分析 (1)由矩形的性质得出∠B=∠C=∠ADC=90°,AB=DC=7,BC=AD=12,证出△DCF是等腰直角三角形,得出FC=DC=7,AB=FC,由ASA证明△ABF≌△FCE,得出EF=AF;
(2)根据BF=BC-FC计算出BF的长,由勾股定理计算即可得出结果.
解答 (1)证明:∵四边形ABCD是矩形,
∴∠B=∠C=∠ADC=90°,AB=DC=7,BC=AD=12,
∴∠BAF+∠AFB=90°,
∵DF平分∠ADC,
∴∠ADF=∠CDF=45°,
∴△DCF是等腰直角三角形,
∴FC=DC=7,
∴AB=FC,
∵AF⊥EF,
∴∠AFE=90°,
∴∠AFB+∠EFC=90°,
∴∠BAF=∠EFC,
在△ABF和△FCE中,
$\left\{\begin{array}{l}{∠BAF=∠EFC}\\{AB=FC}\\{∠B=∠C}\end{array}\right.$,
∴△ABF≌△FCE(ASA),
∴EF=AF;
(2)解:BF=BC-FC=12-7=5,
在Rt△ABF中,由勾股定理得:
AF=$\sqrt{A{B}^{2}+B{F}^{2}}$=$\sqrt{{7}^{2}+{5}^{2}}$=$\sqrt{74}$,
则EF=AF=$\sqrt{74}$.
点评 本题考查了矩形的性质、等腰直角三角形的性质、全等三角形的判定与性质、勾股定理;熟练掌握矩形的性质,并能进行推理计算是解决问题的关键.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
 已知:如图,在△ABC中,∠C=∠ABC=2∠A=4∠DBC.求证:BD⊥AC.
已知:如图,在△ABC中,∠C=∠ABC=2∠A=4∠DBC.求证:BD⊥AC.