题目内容
20.对于题目:“化简并求值:$\frac{1}{a}$+$\sqrt{\frac{1}{{a}^{2}}{+a}^{2}-2}$,其中a=2.”甲、乙两人的解答不同,甲的解答是:$\frac{1}{a}$+$\sqrt{\frac{1}{{a}^{2}}{+a}^{2}-2}$=$\frac{1}{a}$+$\sqrt{{(\frac{1}{a}-a)}^{2}}$=$\frac{1}{a}$+$\frac{1}{a}$-a=$\frac{2}{a}$-a=$\frac{2}{2}$-2=-1;
乙的解答是:$\frac{1}{a}$+$\sqrt{\frac{1}{{a}^{2}}{+a}^{2}-2}$=$\frac{1}{a}$+$\sqrt{{(a-\frac{1}{a})}^{2}}$=$\frac{1}{a}$+a-$\frac{1}{a}$=a=2.
谁的解答是错误的?请说明理由.
分析 根据二次根式的性质判断化简的正确性即可.
解答 解:因为a=2时,$\frac{1}{a}$-a=$\frac{1}{2}$-2=-1$\frac{1}{2}$<0,
所以错误的是甲.
点评 此题考查二次根式的性质,关键是应熟练掌握二次根式的性质.

练习册系列答案
相关题目
15.若一个直角三角形的两边长分别为3和4,则第三边长的平方是( )
| A. | 7 | B. | 14 | C. | 25 | D. | 7或25 |
12.下列各式表示正确的是( )
| A. | $\sqrt{9}$=±3 | B. | ±$\sqrt{9}$=3 | C. | $±\sqrt{9}$=±3 | D. | ±$\sqrt{(-3)^{2}}$=-3 |
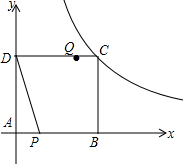 已知正方形ABCD,顶点A与坐标原点重合,顶点B、D分别在x轴和y轴的正半轴上,顶点C在反比例函数y=$\frac{16}{x}$(x>0)的图象上,如图所示,动点P以每秒1个单位的速度从A点出发沿AB方向运动,动点Q同时以每秒4个单位速度从D点出发沿正方形的边DC-CB-BA方向顺时针折线运动,当点P与点Q相遇时停止运动,设点P的运动时间为t.
已知正方形ABCD,顶点A与坐标原点重合,顶点B、D分别在x轴和y轴的正半轴上,顶点C在反比例函数y=$\frac{16}{x}$(x>0)的图象上,如图所示,动点P以每秒1个单位的速度从A点出发沿AB方向运动,动点Q同时以每秒4个单位速度从D点出发沿正方形的边DC-CB-BA方向顺时针折线运动,当点P与点Q相遇时停止运动,设点P的运动时间为t. 如图所示,A(1,0)、点B在y轴上,将三角形OAB沿x轴负方向平移,平移后的图形为三角形DEC,且点C的坐标为(-3,2).
如图所示,A(1,0)、点B在y轴上,将三角形OAB沿x轴负方向平移,平移后的图形为三角形DEC,且点C的坐标为(-3,2).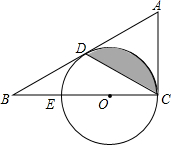 如图,CE是⊙O的直径,AC是⊙O的切线,D为⊙O上的一点,且AD=AC,延长AD交CE的延长线于点B.
如图,CE是⊙O的直径,AC是⊙O的切线,D为⊙O上的一点,且AD=AC,延长AD交CE的延长线于点B.