题目内容
5.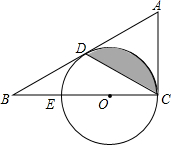 如图,CE是⊙O的直径,AC是⊙O的切线,D为⊙O上的一点,且AD=AC,延长AD交CE的延长线于点B.
如图,CE是⊙O的直径,AC是⊙O的切线,D为⊙O上的一点,且AD=AC,延长AD交CE的延长线于点B.(1)求证:AD为⊙O的切线;
(2)求证:∠A=2∠DCB;
(3)若BE=EO=3,求图中阴影部分的面积(结果保留π).
分析 (1)连接OD,由AD=AC,OD=OC,可得∠ADC=∠ACD,∠ODC=∠OCD,又CA为切线,可知∠ADO=∠ACB=90°,可得AD为切线;
(2)由BE=EO=3,则OB=6,OD=3,所以可得∠B=30°,进而求得∠DOB=60°,∠DOC=120°,再利用扇形COD的面积减去△ODC的面积可求得阴影部分面积.
解答 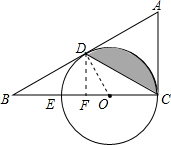 (1)证明:如图,连接OD,∵AD=AC,
(1)证明:如图,连接OD,∵AD=AC,
∴∠ADC=∠ACD,
∵OD=OC,
∴∠ODC=∠OCD,
∴∠ADC+∠ODC=∠ACD+∠OCD,
即∠ADO=∠ACB,
∵CE是⊙O的直径,AC是⊙O的切线,
∴BC⊥AC,
∴∠ADO=∠ACB=90°,
∴AD为⊙O的切线;
(2)证明:如图,∵∠ADC=∠ACD,
∴∠A=180°-2∠ACD,
∵∠ACB=90°,
∴∠ACD=90°-∠DCB
∴∠A=180°-2(90°-∠DCB)=2∠DCB;
(3)如图,∵AD为⊙O的切线,
∴∠ADO=90°,
∵BE=EO=3,
∴BO=6,OD=3,
∴tan∠B=$\frac{OD}{BO}$=$\frac{1}{2}$,
∴∠B=30°,
∴∠DOC=90°+30°=120°,
∴∠BOD=60°,
作DF⊥BC于F,
∴DF=$\frac{\sqrt{3}}{2}$OD=$\frac{3}{2}$$\sqrt{3}$,
∴S扇形COD=$\frac{1}{3}$π•OD2=3π,S△ODC=$\frac{1}{2}$OC•DF=$\frac{1}{2}$×3×$\frac{3}{2}$$\sqrt{3}$=$\frac{9\sqrt{3}}{4}$,
∴S阴影=S扇形COD-S△ODC=3π-$\frac{9\sqrt{3}}{4}$.
点评 本题主要考查切线的性质和判定及扇形的计算,掌握切线问题中的两种辅助线的作法及扇形的面积公式是解题的关键.

| A. | 8 | B. | 10 | C. | 12 | D. | 16 |
| A. | (2,-4) | B. | (6,-4) | C. | (6,-1) | D. | (2,-1) |
| A. | 4×10-7 | B. | 0.4×10-6 | C. | 4×10-6 | D. | 4×10-5 |