题目内容
1.已知方程x2+px+q=0有两个相同的实数根,判断方程x2-p(1+q)x+q3+2q2+q=0的根情况.分析 由方程x2+px+q=0有2个相同的实数根,得到△1=p2-4q=0,而对于方程x2-p(1+q)x+q3+2q2+q=0的判别式△2=[p(1+q)]2-4(q3+2q2+q)=p2(1+q)2-4q(1+q)2=(p2-4q)(1+q)2,故△2=0,结论得证.
解答 解:∵方程x2+px+q=0有2个相同的实数根,
∴△1=p2-4q=0,
而对于方程x2-p(1+q)x+q3+2q2+q=0,
其判别式△2=[p(1+q)]2-4(q3+2q2+q)
=p2(1+q)2-4q(1+q)2
=(p2-4q)(1+q)2=0,
∴方程x2-p(1+q)x+q3+2q2+q=0有2个相同的实数根.
点评 本题主要考查了一元二次方程根的判别式:△=b2-4ac,当△>0时方程有两个不等实根,△=0时方程有两个相等实根,△<0时方程没有实根.

练习册系列答案
 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
12.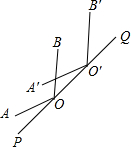 如图,点O在直线PQ上,∠AOP=20°,将∠AOB沿PQ方向平移一段距离后得到∠A′O′B′,且有∠B′O′Q=40°,则∠AOB的度数为( )
如图,点O在直线PQ上,∠AOP=20°,将∠AOB沿PQ方向平移一段距离后得到∠A′O′B′,且有∠B′O′Q=40°,则∠AOB的度数为( )
 如图,点O在直线PQ上,∠AOP=20°,将∠AOB沿PQ方向平移一段距离后得到∠A′O′B′,且有∠B′O′Q=40°,则∠AOB的度数为( )
如图,点O在直线PQ上,∠AOP=20°,将∠AOB沿PQ方向平移一段距离后得到∠A′O′B′,且有∠B′O′Q=40°,则∠AOB的度数为( )| A. | 120° | B. | 140° | C. | 150° | D. | 160° |
10.(-5)2013+(-5)2012能被下列数整除的是( )
| A. | 4 | B. | 6 | C. | 9 | D. | 15 |