题目内容
14.5月9号重庆实验外国语学校就行了“五四表彰大会”,初三某班老师准备从包括小明在内的四名优秀团员中,随机抽取了2名学生参加表彰大会,则抽到小明的概率是( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{6}$ |
分析 由初三某班老师准备从包括小明在内的四名优秀团员中,随机抽取了2名学生参加表彰大会,直接利用概率公式求解即可求得答案.
解答 解:∵初三某班老师准备从包括小明在内的四名优秀团员中,随机抽取了2名学生参加表彰大会,
∴抽到小明的概率是:$\frac{2}{4}$=$\frac{1}{2}$.
故选A.
点评 此题考查了概率公式的应用.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
相关题目
4.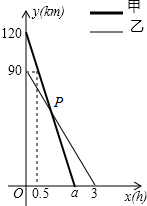 在一条笔直的公路旁依次有A、B、C三个村庄,甲、乙两人同时分别从A、B两村出发,甲骑摩托车,乙骑电动车沿公路匀速驶向C村,最终到达C村.甲、乙两人到C村的距离y1,y2(km)与行驶时间x(h)之间的函数关系如图所示,以下分析错误的是( )
在一条笔直的公路旁依次有A、B、C三个村庄,甲、乙两人同时分别从A、B两村出发,甲骑摩托车,乙骑电动车沿公路匀速驶向C村,最终到达C村.甲、乙两人到C村的距离y1,y2(km)与行驶时间x(h)之间的函数关系如图所示,以下分析错误的是( )
 在一条笔直的公路旁依次有A、B、C三个村庄,甲、乙两人同时分别从A、B两村出发,甲骑摩托车,乙骑电动车沿公路匀速驶向C村,最终到达C村.甲、乙两人到C村的距离y1,y2(km)与行驶时间x(h)之间的函数关系如图所示,以下分析错误的是( )
在一条笔直的公路旁依次有A、B、C三个村庄,甲、乙两人同时分别从A、B两村出发,甲骑摩托车,乙骑电动车沿公路匀速驶向C村,最终到达C村.甲、乙两人到C村的距离y1,y2(km)与行驶时间x(h)之间的函数关系如图所示,以下分析错误的是( )| A. | A、C两村间的距离为120km | |
| B. | 点P的坐标为(1,60) | |
| C. | 点P的意义表示经过1小时甲与乙相遇且距C村60km | |
| D. | 乙在行驶过程中,仅有一次机会距甲10km |
5.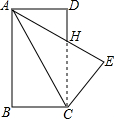 如图,矩形ABCD中,AB=4,BC=3,将矩形ABCD沿AC折叠,则重叠部分面积为( )
如图,矩形ABCD中,AB=4,BC=3,将矩形ABCD沿AC折叠,则重叠部分面积为( )
 如图,矩形ABCD中,AB=4,BC=3,将矩形ABCD沿AC折叠,则重叠部分面积为( )
如图,矩形ABCD中,AB=4,BC=3,将矩形ABCD沿AC折叠,则重叠部分面积为( )| A. | $\frac{25}{8}$ | B. | $\frac{75}{8}$ | C. | $\frac{75}{16}$ | D. | $\frac{25}{4}$ |
9.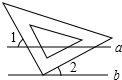 如图,已知a∥b,三角板的直角顶点在直线b上,∠1=54°,那么∠2等于( )
如图,已知a∥b,三角板的直角顶点在直线b上,∠1=54°,那么∠2等于( )
 如图,已知a∥b,三角板的直角顶点在直线b上,∠1=54°,那么∠2等于( )
如图,已知a∥b,三角板的直角顶点在直线b上,∠1=54°,那么∠2等于( )| A. | 45° | B. | 36° | C. | 54° | D. | 126° |
3. 根据四边形的不稳定性,当变动∠B的度数时,菱形ABCD的形状会发生改变,当∠B=60°时,如图1,AC=$\sqrt{2}$;当∠B=90°时,如图2,AC=( )
根据四边形的不稳定性,当变动∠B的度数时,菱形ABCD的形状会发生改变,当∠B=60°时,如图1,AC=$\sqrt{2}$;当∠B=90°时,如图2,AC=( )
 根据四边形的不稳定性,当变动∠B的度数时,菱形ABCD的形状会发生改变,当∠B=60°时,如图1,AC=$\sqrt{2}$;当∠B=90°时,如图2,AC=( )
根据四边形的不稳定性,当变动∠B的度数时,菱形ABCD的形状会发生改变,当∠B=60°时,如图1,AC=$\sqrt{2}$;当∠B=90°时,如图2,AC=( )| A. | $\sqrt{2}$ | B. | 2 | C. | 2$\sqrt{2}$ | D. | $\sqrt{3}$ |
4.不等式组$\left\{\begin{array}{l}{2x-1<1}\\{-x≤2}\end{array}\right.$的解集为( )
| A. | -2<x<1 | B. | x<1 | C. | -2≤x<1 | D. | x≥-2 |
 如图,用若干个全等的正五边形可以拼成一个环状,图中所示的是前3个正五边形的拼接情况,要完全拼成一个圆环还需要的正五边形个数是( )
如图,用若干个全等的正五边形可以拼成一个环状,图中所示的是前3个正五边形的拼接情况,要完全拼成一个圆环还需要的正五边形个数是( )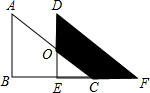 如图,两个全等的直角三角形重叠在一起,将Rt△ABC沿着BC的方向平移到Rt△DEF的位置,已知AB=5,DO=2,平移距离为3,则阴影部分的面积为( )
如图,两个全等的直角三角形重叠在一起,将Rt△ABC沿着BC的方向平移到Rt△DEF的位置,已知AB=5,DO=2,平移距离为3,则阴影部分的面积为( ) 如图是由四个小正方体搭成的一个几何体,这个几何体的俯视图是( )
如图是由四个小正方体搭成的一个几何体,这个几何体的俯视图是( )


