题目内容
5.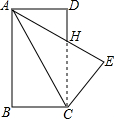 如图,矩形ABCD中,AB=4,BC=3,将矩形ABCD沿AC折叠,则重叠部分面积为( )
如图,矩形ABCD中,AB=4,BC=3,将矩形ABCD沿AC折叠,则重叠部分面积为( )| A. | $\frac{25}{8}$ | B. | $\frac{75}{8}$ | C. | $\frac{75}{16}$ | D. | $\frac{25}{4}$ |
分析 因为AD为CH边上的高,要求△ACH的面积,求得HC即可,先证△ADH≌△HEC,得AH=HC,设AH=x,则在Rt△ADH中,根据勾股定理求x,解答即可.
解答 解:根据翻折的性质可知:BC=EC=AD,∠D=∠E,∠AHD=∠CHE,
∴△ADH≌△HEC,
∴AH=HC,
设HC=x,则DH=4-x,
在Rt△ADH中,AH2=DH2+AD2,即为x2=(4-x)2+32,
解之得:x=$\frac{25}{8}$,
∴S△AHC=$\frac{1}{2}$•HC•AD=$\frac{1}{2}$×3×$\frac{25}{8}$=$\frac{75}{16}$,
故选:C.
点评 本题考查了翻折变换的知识及勾股定理的正确运用,本题中设HC=x,根据直角三角形ADH中运用勾股定理求x是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
16.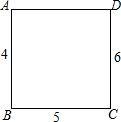 如图所示,在正方形ABCD的每个顶点上写一个数,把这个正方形每条边的两端点上的数加起来,将和写在这条边上,已知AB上的数为4,BC上的数为5,CD上的数为6,则AD上的数应为( )
如图所示,在正方形ABCD的每个顶点上写一个数,把这个正方形每条边的两端点上的数加起来,将和写在这条边上,已知AB上的数为4,BC上的数为5,CD上的数为6,则AD上的数应为( )
 如图所示,在正方形ABCD的每个顶点上写一个数,把这个正方形每条边的两端点上的数加起来,将和写在这条边上,已知AB上的数为4,BC上的数为5,CD上的数为6,则AD上的数应为( )
如图所示,在正方形ABCD的每个顶点上写一个数,把这个正方形每条边的两端点上的数加起来,将和写在这条边上,已知AB上的数为4,BC上的数为5,CD上的数为6,则AD上的数应为( )| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
13. 如图,沿AC方向修山路,为了加快施工进度,要在小山的另一边同时施工,从AC上的一点B取∠ABD=145°,BD=500米,∠D=55°,使A、C、E在一条直线上,那么开挖点E与D的距离是( )
如图,沿AC方向修山路,为了加快施工进度,要在小山的另一边同时施工,从AC上的一点B取∠ABD=145°,BD=500米,∠D=55°,使A、C、E在一条直线上,那么开挖点E与D的距离是( )
 如图,沿AC方向修山路,为了加快施工进度,要在小山的另一边同时施工,从AC上的一点B取∠ABD=145°,BD=500米,∠D=55°,使A、C、E在一条直线上,那么开挖点E与D的距离是( )
如图,沿AC方向修山路,为了加快施工进度,要在小山的另一边同时施工,从AC上的一点B取∠ABD=145°,BD=500米,∠D=55°,使A、C、E在一条直线上,那么开挖点E与D的距离是( )| A. | 500sin55°米 | B. | 500cos35°米 | C. | 500cos55°米 | D. | 500tan55°米 |
10.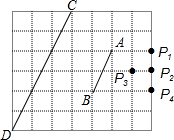 如图6×7的方格中,点A,B,C,D是格点,线段CD是由线段AB位似放大得到的,则它们的位似中心是( )
如图6×7的方格中,点A,B,C,D是格点,线段CD是由线段AB位似放大得到的,则它们的位似中心是( )
 如图6×7的方格中,点A,B,C,D是格点,线段CD是由线段AB位似放大得到的,则它们的位似中心是( )
如图6×7的方格中,点A,B,C,D是格点,线段CD是由线段AB位似放大得到的,则它们的位似中心是( )| A. | P1 | B. | P2 | C. | P3 | D. | P4 |
17.某市5月份日平均气温统计如下表,则在日平均气温这组数据中,众数和中位数分别是( )
| 日平均气温(℃) | 20 | 21 | 22 | 23 | 24 |
| 天数 | 4 | 10 | 8 | 6 | 2 |
| A. | 21,21 | B. | 21,21.5 | C. | 21,22 | D. | 22,22 |
14.5月9号重庆实验外国语学校就行了“五四表彰大会”,初三某班老师准备从包括小明在内的四名优秀团员中,随机抽取了2名学生参加表彰大会,则抽到小明的概率是( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{6}$ |
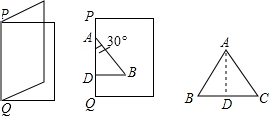 如图,欢欢将一张白纸对折,折痕为PQ.以PQ上的线段AD为一条直角边画出直角三角形ABD,使∠DAB=30°,沿折线DBA剪下三角形纸片,将其打开展平,得到△ABC.
如图,欢欢将一张白纸对折,折痕为PQ.以PQ上的线段AD为一条直角边画出直角三角形ABD,使∠DAB=30°,沿折线DBA剪下三角形纸片,将其打开展平,得到△ABC.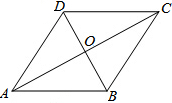 如图,菱形ABCD中,点O是对角线AC、BD的交点,已知AB=5,OB=3,则菱形ABCD的面积是24.
如图,菱形ABCD中,点O是对角线AC、BD的交点,已知AB=5,OB=3,则菱形ABCD的面积是24.