题目内容
4.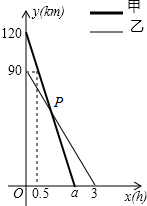 在一条笔直的公路旁依次有A、B、C三个村庄,甲、乙两人同时分别从A、B两村出发,甲骑摩托车,乙骑电动车沿公路匀速驶向C村,最终到达C村.甲、乙两人到C村的距离y1,y2(km)与行驶时间x(h)之间的函数关系如图所示,以下分析错误的是( )
在一条笔直的公路旁依次有A、B、C三个村庄,甲、乙两人同时分别从A、B两村出发,甲骑摩托车,乙骑电动车沿公路匀速驶向C村,最终到达C村.甲、乙两人到C村的距离y1,y2(km)与行驶时间x(h)之间的函数关系如图所示,以下分析错误的是( )| A. | A、C两村间的距离为120km | |
| B. | 点P的坐标为(1,60) | |
| C. | 点P的意义表示经过1小时甲与乙相遇且距C村60km | |
| D. | 乙在行驶过程中,仅有一次机会距甲10km |
分析 A、由图可知与y轴交点的坐标表示A、C两村间的距离为120km,再由0.5小时距离C村90km,行驶120-90=30km,速度为60km/h,求得a=2;
B、求得y1,y2两个函数解析式,建立方程求得点P坐标;
C、点P表示在什么时间相遇以及距离C村的距离;
D、由B中的函数解析式根据距甲10km建立方程;探讨得出答案即可.
解答 解:A、A、C两村间的距离120km,
a=120÷[(120-90)÷0.5]=2,故A不符合题意;
B、设y1=k1x+120,
代入(2,0)解得y1=-60x+120,
y2=k2x+90,
代入(3,0)解得y1=-30x+90,
由-60x+120=-30x+90
解得x=1,则y1=y2=60,
所以P(1,60),故B不符合题意;
C、点P表示经过1小时甲与乙相遇且距C村60km,故C不符合题意;
D、当y1-y2=10,
即-60x+120-(-30x+90)=10
解得x=$\frac{2}{3}$,
当y2-y1=10,
即-30x+90-(-60x+120)=10
解得x=$\frac{4}{3}$,
当甲走到C地,而乙距离C地10km时,
-30x+90=10
解得x=$\frac{8}{3}$;
综上所知当x=$\frac{2}{3}$h,或x=$\frac{4}{3}$h,或x=$\frac{8}{3}$h乙距甲10km,故D符合题意.
故选:D.
点评 此题考查一次函数的运用,一次函数与二元一次方程组的运用,解答时认真分析图象求出解析式是关键,注意分类思想的渗透.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
12.一个口袋中有 3 个黑球和若干个白球,在不允许将球倒出来数的前提下,小明为估计其中的白球数,采用了如下的方法:从口袋中随机摸出一球,记下颜色,然后把它放回口袋中,摇匀后再随机摸出一球,记下颜色,…,不断重复上述过程.小明共摸了100次,其中25次摸到黑球.根据上述数据,小明可估计口袋中的白球大约有( )
| A. | 12 个 | B. | 15 个 | C. | 9 个 | D. | 10 个 |
16.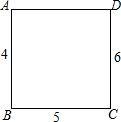 如图所示,在正方形ABCD的每个顶点上写一个数,把这个正方形每条边的两端点上的数加起来,将和写在这条边上,已知AB上的数为4,BC上的数为5,CD上的数为6,则AD上的数应为( )
如图所示,在正方形ABCD的每个顶点上写一个数,把这个正方形每条边的两端点上的数加起来,将和写在这条边上,已知AB上的数为4,BC上的数为5,CD上的数为6,则AD上的数应为( )
 如图所示,在正方形ABCD的每个顶点上写一个数,把这个正方形每条边的两端点上的数加起来,将和写在这条边上,已知AB上的数为4,BC上的数为5,CD上的数为6,则AD上的数应为( )
如图所示,在正方形ABCD的每个顶点上写一个数,把这个正方形每条边的两端点上的数加起来,将和写在这条边上,已知AB上的数为4,BC上的数为5,CD上的数为6,则AD上的数应为( )| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
13. 如图,沿AC方向修山路,为了加快施工进度,要在小山的另一边同时施工,从AC上的一点B取∠ABD=145°,BD=500米,∠D=55°,使A、C、E在一条直线上,那么开挖点E与D的距离是( )
如图,沿AC方向修山路,为了加快施工进度,要在小山的另一边同时施工,从AC上的一点B取∠ABD=145°,BD=500米,∠D=55°,使A、C、E在一条直线上,那么开挖点E与D的距离是( )
 如图,沿AC方向修山路,为了加快施工进度,要在小山的另一边同时施工,从AC上的一点B取∠ABD=145°,BD=500米,∠D=55°,使A、C、E在一条直线上,那么开挖点E与D的距离是( )
如图,沿AC方向修山路,为了加快施工进度,要在小山的另一边同时施工,从AC上的一点B取∠ABD=145°,BD=500米,∠D=55°,使A、C、E在一条直线上,那么开挖点E与D的距离是( )| A. | 500sin55°米 | B. | 500cos35°米 | C. | 500cos55°米 | D. | 500tan55°米 |
14.5月9号重庆实验外国语学校就行了“五四表彰大会”,初三某班老师准备从包括小明在内的四名优秀团员中,随机抽取了2名学生参加表彰大会,则抽到小明的概率是( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{6}$ |
 如图,已知BE=CD,要使△ABE≌△ACD,要添加一个条件是∠B=∠C.(只填一种情况).
如图,已知BE=CD,要使△ABE≌△ACD,要添加一个条件是∠B=∠C.(只填一种情况).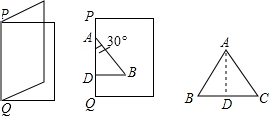 如图,欢欢将一张白纸对折,折痕为PQ.以PQ上的线段AD为一条直角边画出直角三角形ABD,使∠DAB=30°,沿折线DBA剪下三角形纸片,将其打开展平,得到△ABC.
如图,欢欢将一张白纸对折,折痕为PQ.以PQ上的线段AD为一条直角边画出直角三角形ABD,使∠DAB=30°,沿折线DBA剪下三角形纸片,将其打开展平,得到△ABC.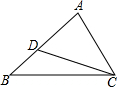 如图,在△ABC中,AB=10,AC=8,点D在边AB上,若∠ACD=∠B,则AD的长为6.4.
如图,在△ABC中,AB=10,AC=8,点D在边AB上,若∠ACD=∠B,则AD的长为6.4.