题目内容
12.给定关于x的二次函数y=2x2+(6-2m)x+3-m,学生甲:当m=3时,抛物线与x轴只有一个交点,因此当抛物线与x轴只有一个交点时,m的值为3;
学生乙:如果抛物线在x轴上方,那么该抛物线的最低点一定在第二象限;
请判断学生甲、乙的观点是否正确,并说明你的理由.
分析 甲的观点是错误的,乙的观点是正确的.分别求出抛物线y=2x2+(6-2m)x+3-m与x轴只有一个交点时m的值以及抛物线在x轴上方时该抛物线的最低点的位置即可.
解答 解:甲的观点是错误的.
理由如下:当抛物线y=2x2+(6-2m)x+3-m与x轴只有一个交点时(6-2m)2-4×2×(3-m)=0,
即:(3-m)(4-4m)=0,
解得m=3或m=1,
即m=3或m=1时抛物线y=2x2+(6-2m)x+3-m与x轴只有一个交点;
乙的观点是正确的,
理由如下:当抛物线在x轴上方时,
由上可得(6-2m)2-4×2×(3-m)<0,
即:(3-m)(4-4m)<0,
∴1<m<3,
而对于开口向上的抛物线最低点为其顶点,
顶点的横坐标为$x=-\frac{6-2m}{2×2}=\frac{m-3}{2}$,
∵1<m<3,
∴$x=\frac{m-3}{2}<0$,且抛物线在x轴上方
即抛物线的最低点在第二象限.
点评 本题考查了抛物线和x轴交点问题以及和二次函数有关的性质,求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标,令y=0,即ax2+bx+c=0,解关于x的一元二次方程即可求得交点横坐标.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.圆内接正六边形的边长为3,则该圆内接正三角形的边长为( )
| A. | $6\sqrt{2}$ | B. | $3\sqrt{3}$ | C. | $6\sqrt{3}$ | D. | $3\sqrt{2}$ |
2.用加减消元法解二元一次方程组$\left\{\begin{array}{l}{2x-3y=7①}\\{5x-3y=-2②}\end{array}\right.$,由①-②可得的方程为( )
| A. | 3x=5 | B. | -3x=9 | C. | -3x-6y=9 | D. | 3x-6y=5 |
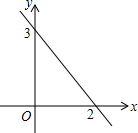 一次函数y=kx+b(k≠0)的图象如图所示,当x=0时,y的值是3.
一次函数y=kx+b(k≠0)的图象如图所示,当x=0时,y的值是3.
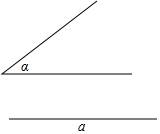 如图,已知∠α和线段a,求作△ABC,使BC=a,∠B=∠C=$\frac{1}{2}$α(只保留作图痕迹,不要求写出作法)
如图,已知∠α和线段a,求作△ABC,使BC=a,∠B=∠C=$\frac{1}{2}$α(只保留作图痕迹,不要求写出作法)