题目内容
18.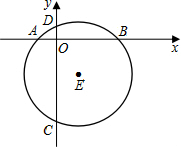 如图,在直角坐标系中,⊙E的半径为5,点E(1,-4).
如图,在直角坐标系中,⊙E的半径为5,点E(1,-4).(1)求弦AB与弦CD的长;
(2)求点A,B坐标.
分析 (1)先过E作EF⊥AB于F,作EG⊥CD于G,根据垂径定理得出BF=$\frac{1}{2}$AB,CG=$\frac{1}{2}$CD,再根据⊙E的半径为5,E(1,-4),运用勾股定理求得BF和CG的长,即可得出弦AB与弦CD的长;
(2)先根据E(1,-4),EF⊥AB,得出F(1,0),再根据AF=BF=3,即可得出OB=1+3=4,AO=3-1=2,进而得到点A,B坐标.
解答  解:(1)如图所示,过E作EF⊥AB于F,作EG⊥CD于G,则BF=$\frac{1}{2}$AB,CG=$\frac{1}{2}$CD,
解:(1)如图所示,过E作EF⊥AB于F,作EG⊥CD于G,则BF=$\frac{1}{2}$AB,CG=$\frac{1}{2}$CD,
∵⊙E的半径为5,E(1,-4),
∴BE=5,EF=4,GE=1,
∴Rt△BEF中,BF=$\sqrt{{5}^{2}-{4}^{2}}$=3,
Rt△CEG中,CG=$\sqrt{{5}^{2}-{1}^{2}}$=2$\sqrt{6}$,
∴AB=2BF=6,CD=2CG=4$\sqrt{6}$;
(2)如图所示,∵E(1,-4),EF⊥AB,
∴F(1,0),
又∵AF=BF=3,
∴OB=1+3=4,AO=3-1=2,
∴A(-2,0),B(4,0).
点评 本题主要考查了垂径定理与勾股定理的运用,解决问题的关键是作辅助线构造直角三角形,运用垂径定理以及勾股定理求得线段的长度.

练习册系列答案
相关题目
10.某公园的门票是10元/人,团体购票有如下优惠:
某校七年级两个班到该公园秋游,其中甲班多于30人,乙班不足30人,如果以班为单位分别购票,两个班一共应付598元.如果两个班作为一个团体购票,一共应付545元,则甲班有36人,乙班有25人.
| 购票人数 | 1-30人 | 31-60人 | 60人以上 |
| 票价 | 无折扣 | 超出30人的部分,票价打八折 | 超出60人的部分,票价打五折 |
5.如果两个有理数的积是正数,那么这两个有理数( )
| A. | 同号,且均为负数 | B. | 异号 | C. | 同号,且均为正数 | D. | 同号 |
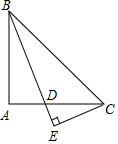 已知:△ABC是等腰直角三角形,∠BAC=90°,BD平分∠ABC交AC于点D,CE垂直于BD,交BD的延长线于点E,求证:BD=2CE.
已知:△ABC是等腰直角三角形,∠BAC=90°,BD平分∠ABC交AC于点D,CE垂直于BD,交BD的延长线于点E,求证:BD=2CE. 如图,⊙O是△ABC的内切圆,点D,E,F为切点.
如图,⊙O是△ABC的内切圆,点D,E,F为切点.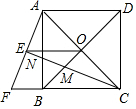 如图,正方形ABCD的对角线AC,BD相交于点O,延长CB至点F,使CF=CA,连接AF,∠ACF的平分线分别交AF,AB,BD于点E,N,M,连接EO.
如图,正方形ABCD的对角线AC,BD相交于点O,延长CB至点F,使CF=CA,连接AF,∠ACF的平分线分别交AF,AB,BD于点E,N,M,连接EO.