题目内容
10.某公园的门票是10元/人,团体购票有如下优惠:| 购票人数 | 1-30人 | 31-60人 | 60人以上 |
| 票价 | 无折扣 | 超出30人的部分,票价打八折 | 超出60人的部分,票价打五折 |
分析 设甲班有x人,乙班有y人,根据“①超出60人部分的费用=545-(300+30×10×0.8)、②乙班费用+甲班费用=598”列方程组求解可得.
解答 解:设甲班有x人,乙班有y人,
根据题意可得$\left\{\begin{array}{l}{(x+y-60)×5=545-540}\\{10y+300+(x-30)×8=598}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=36}\\{y=25}\end{array}\right.$,
即甲班有36人,乙班有25人,
故答案为:36,25.
点评 本题主要考查二元一次方程组的应用,弄清表格中分段收费标准,根据费用确定其中蕴含的相等关系:①超出60人部分的费用=545-(300+30×10×0.8)、②乙班费用+甲班费用=598是解题的关键.

练习册系列答案
相关题目
15.一次越野赛跑中,当小明跑了1600m时,小刚跑了1450m.此后两人分别以am/s和bm/s匀速跑.又过100s时小刚追上小明,200s时小刚到达终点,300s时小明到达终点.求这次越野赛跑的全程.
(Ⅰ)根据题意,填写下表:
(Ⅱ)求出问题的解.
(Ⅰ)根据题意,填写下表:
| 时间(秒) 路程(米) | 从比赛开始到 匀速跑前 | 从比赛开始到 匀速跑完100秒 | 从比赛开始到 匀速跑完200秒 |
| 小明 | 1600 | 1600+100a | 1600+200a |
| 小刚 | 1450 | 1450+100b | 1450+200b |
2.已知△ABC的三边长a、b、c满足a2+|$\sqrt{50}$-c|=10a-25-$\sqrt{5-b}$,则对△ABC的形状描述最准确的是( )
| A. | 等腰三角形 | B. | 直角三角形 | C. | 等腰直角三角形 | D. | 等边三角形 |

 ∠COB。
∠COB。 如图,AB是⊙O直径,弦AD、BC相交于点E,若CD=5,AB=13,则$\frac{DE}{BE}$=$\frac{5}{13}$.
如图,AB是⊙O直径,弦AD、BC相交于点E,若CD=5,AB=13,则$\frac{DE}{BE}$=$\frac{5}{13}$.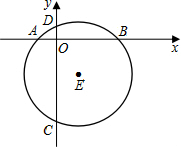 如图,在直角坐标系中,⊙E的半径为5,点E(1,-4).
如图,在直角坐标系中,⊙E的半径为5,点E(1,-4).