题目内容
13.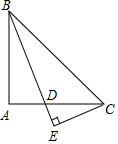 已知:△ABC是等腰直角三角形,∠BAC=90°,BD平分∠ABC交AC于点D,CE垂直于BD,交BD的延长线于点E,求证:BD=2CE.
已知:△ABC是等腰直角三角形,∠BAC=90°,BD平分∠ABC交AC于点D,CE垂直于BD,交BD的延长线于点E,求证:BD=2CE.
分析 延长BA和CE交于点M,首先证明△BME≌△BCE可得EM=EC=$\frac{1}{2}$MC,再证明△ABD≌△ACM可得DB=MC,利用等量代换可得BD=2CE.
解答  证明:延长BA和CE交于点M,
证明:延长BA和CE交于点M,
∵CE⊥BD,
∴∠BEC=∠BEM=90°,
∵BD平分∠ABC,
∴∠MBE=∠CBE,
在△BME和△BCE中$\left\{\begin{array}{l}{∠CBE=∠MBE}\\{BE=BE}\\{∠BEM=∠BEC}\end{array}\right.$,
∴△BME≌△BCE(ASA),
∴EM=EC=$\frac{1}{2}$MC,
∵△ABC是等腰直角三角形,
∴∠BAC=∠MAC=90°,BA=AC,
∴∠ABD+∠BDA=90°,
∵∠BEC=90°,
∴∠ACM+∠CBE=90°,
∵∠BDA=∠EDC,
∴∠ABE=∠ACM,
在△ABD和△ACM中$\left\{\begin{array}{l}{∠ABD=∠ACM}\\{AB=AC}\\{∠BAC=∠MAC}\end{array}\right.$,
∴△ABD≌△ACM(ASA),
∴DB=MC,
∴BD=2CE.
点评 此题主要考查了全等三角形的判定和性质,以及等腰直角三角形的性质,关键是正确证明EM=EC=$\frac{1}{2}$MC和DB=MC.

练习册系列答案
 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
2.已知△ABC的三边长a、b、c满足a2+|$\sqrt{50}$-c|=10a-25-$\sqrt{5-b}$,则对△ABC的形状描述最准确的是( )
| A. | 等腰三角形 | B. | 直角三角形 | C. | 等腰直角三角形 | D. | 等边三角形 |
20.若二次根式$\sqrt{x-6}$在实数范围内有意义,则x的取值范围是( )
| A. | x≥6 | B. | x>6 | C. | x>-6 | D. | x≤6 |
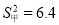 ,乙同学的方差是
,乙同学的方差是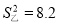 ,那么这两名同学跳高成绩比较稳定的是_____同学.
,那么这两名同学跳高成绩比较稳定的是_____同学. 如图,AB是⊙O直径,弦AD、BC相交于点E,若CD=5,AB=13,则$\frac{DE}{BE}$=$\frac{5}{13}$.
如图,AB是⊙O直径,弦AD、BC相交于点E,若CD=5,AB=13,则$\frac{DE}{BE}$=$\frac{5}{13}$.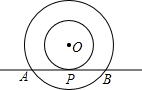 如图,以点O为圆心的两个同心圆中,大圆的弦AB切小圆于点P.
如图,以点O为圆心的两个同心圆中,大圆的弦AB切小圆于点P.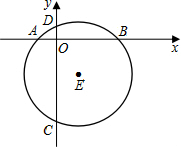 如图,在直角坐标系中,⊙E的半径为5,点E(1,-4).
如图,在直角坐标系中,⊙E的半径为5,点E(1,-4).
