题目内容
7.在平面直角坐标系内有两点A、B,其坐标为A(-1,-1),B(2,4),点M为x轴上的一个动点,若要使MB-MA的值最大,则点M的坐标为(-2,0).分析 利用轴对称图形的性质可作点A关于x轴的对称点A′,连接A′B,交x轴于点M,点M即为所求.
解答 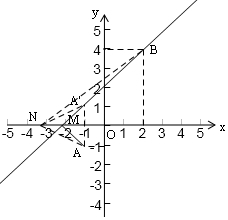 解:作点A(-1,-1)关于x轴的对称点A′(-1,1),作直线A′B交x轴于点M,
解:作点A(-1,-1)关于x轴的对称点A′(-1,1),作直线A′B交x轴于点M,
由对称性知:MA′=MA,
∴MB-MA=MB-MA′=A′B,
若N是x轴上异于M的点,则NA′=NA,这时NB-NA=NB-NA′<A′B=MB-MA′,
所以,点M就是使MB-MA的值最大的点,MB-MA的最大值是A′B,
设直线A′B的解析式为:y=kx+b,
把A′(-1,1),B(2,4)代入得:$\left\{\begin{array}{l}{-k+b=1}\\{2k+b=4}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=1}\\{b=2}\end{array}\right.$,
∴直线A′B的解析式为y=x+2,
∵点M为直线A′B与x轴的交点,
当y=0时,x+2=0,
x=-2,
∴点M的坐标为(-2,0).
故答案为:(-2,0).
点评 本题是求最值问题,考查了在直线上求作一点,使到直线两侧点的距离差最大,涉及待定系数法求一次函数的解析式及在三角形中任意两边之差小于第三边的应用,正确作出一个点的对称点是解题的关键.

练习册系列答案
相关题目
15.一次越野赛跑中,当小明跑了1600m时,小刚跑了1450m.此后两人分别以am/s和bm/s匀速跑.又过100s时小刚追上小明,200s时小刚到达终点,300s时小明到达终点.求这次越野赛跑的全程.
(Ⅰ)根据题意,填写下表:
(Ⅱ)求出问题的解.
(Ⅰ)根据题意,填写下表:
| 时间(秒) 路程(米) | 从比赛开始到 匀速跑前 | 从比赛开始到 匀速跑完100秒 | 从比赛开始到 匀速跑完200秒 |
| 小明 | 1600 | 1600+100a | 1600+200a |
| 小刚 | 1450 | 1450+100b | 1450+200b |
2.已知△ABC的三边长a、b、c满足a2+|$\sqrt{50}$-c|=10a-25-$\sqrt{5-b}$,则对△ABC的形状描述最准确的是( )
| A. | 等腰三角形 | B. | 直角三角形 | C. | 等腰直角三角形 | D. | 等边三角形 |
 ;
; .
. 如图,圆O的半径为2$\sqrt{2}$,AB、AC是圆O的两条弦,AB=2$\sqrt{3}$,AC=4,如果以O为圆心,作一个与AC相切的圆,那么这个圆的半径是多少?它与AB又怎样的位置关系?为什么?
如图,圆O的半径为2$\sqrt{2}$,AB、AC是圆O的两条弦,AB=2$\sqrt{3}$,AC=4,如果以O为圆心,作一个与AC相切的圆,那么这个圆的半径是多少?它与AB又怎样的位置关系?为什么?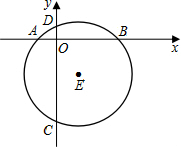 如图,在直角坐标系中,⊙E的半径为5,点E(1,-4).
如图,在直角坐标系中,⊙E的半径为5,点E(1,-4).