��Ŀ����
7������ͼ������������ڲ������֮�Ϳ���֤�����ɶ�����
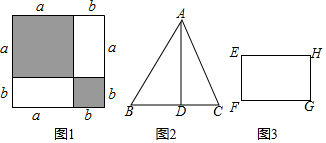
����ͼ��1����ʾ����֤�����ɶ�������Ϊ�������������ʾΪ��a+b��2���ֿɱ�ʾΪc2+4��$\frac{1}{2}$ab�����ԣ�a+b��2=c2+4��$\frac{1}{2}$ab������a2+b2+2ab=c2+2ab������a2+b2=c2����ֱ����������ֱ�DZߵ�ƽ���͵���б�ߵ�ƽ����
��������20����ͳ٤�ƶ�������ͼ��2��֤���˹��ɶ����������âٵķ���֤�����ɶ�����
����ͼ��3�������âٵķ���֤�����ɶ�����
����ͼ��4�������âٵķ���֤�����ɶ�����
���� �����ε�������������ε������ʽ�����Ҳ����������ֱ��������������������������������г���ϵʽ�����ɵ�֤��
������DB������D��BC���ϵĸ�DF����DF=EC=b-a����S�ı���ADCB=S��ACD+S��ABC��S�ı���ADCB=S��ADB+S��DCB�г���ϵʽ�����ɵ�֤��
�ܸ������⣬���ǿ���ͼ���ҵ�����ϵ�����м��С�����ε�������ڴ������ε������ȥ�ĸ�ֱ�������ε�������г���ʽ���ɵó����ɶ����ı���ʽ����
��� 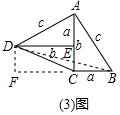 �⣺�����ε����Ϊ$\frac{1}{2}$��a+b����a+b��=$\frac{1}{2}$a2+ab+$\frac{1}{2}$b2��
�⣺�����ε����Ϊ$\frac{1}{2}$��a+b����a+b��=$\frac{1}{2}$a2+ab+$\frac{1}{2}$b2��
Ҳ�����ñ�ʾΪ$\frac{1}{2}$ab+$\frac{1}{2}$c2+$\frac{1}{2}$ab��
��$\frac{1}{2}$a2+ab+$\frac{1}{2}$b2=$\frac{1}{2}$ab+$\frac{1}{2}$c2+$\frac{1}{2}$ab����a2+b2=c2
������DB������D��BC���ϵĸ�DF����DF=EC=b-a
��S�ı���ADCB=S��ACD+S��ABC=$\frac{1}{2}$b2+$\frac{1}{2}$ab��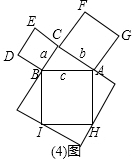 �֡�S�ı���ADCB=S��ADB+S��DCB=$\frac{1}{2}$c2+$\frac{1}{2}$a��b-a��
�֡�S�ı���ADCB=S��ADB+S��DCB=$\frac{1}{2}$c2+$\frac{1}{2}$a��b-a��
��$\frac{1}{2}$b2+$\frac{1}{2}$ab=$\frac{1}{2}$c2+$\frac{1}{2}$a��b-a����
��a2+b2=c2��
�ܸ������⣬�м�С�����ε����c2=��a+b��2-4��$\frac{1}{2}$��ab=a2+b2��
����ֱ����������б�ߵ�ƽ��������ֱ�DZߵ�ƽ���ͣ�
���� ���⿼���˹��ɶ�����֤�������ɶ���������ʽ�ij˷��������Լ��ɶ���ʽ��ͼ�εĴ������ͣ�����֤��Ҫת����ͬһ��ͼ�ε����ֱ�ʾ�������Ӷ�ת���ɷ��̴ﵽ֤���Ľ����

 ��Ȥ������ҵ���ϿƼ�������ϵ�д�
��Ȥ������ҵ���ϿƼ�������ϵ�д�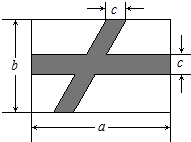 ��ͼ��ʾ���ڹ������οյ��ϣ�Ҫ������·��ͼ�е���Ӱ��ʾ��������ͼ�б�����ݣ�����ͼ�пհײ��ֵ����Ϊ��������
��ͼ��ʾ���ڹ������οյ��ϣ�Ҫ������·��ͼ�е���Ӱ��ʾ��������ͼ�б�����ݣ�����ͼ�пհײ��ֵ����Ϊ��������| A�� | ab-bc-ac+c2 | B�� | bc-ab+ac | C�� | b2-bc+a2-ab | D�� | a2+ab+bc-ac |
| A�� | 4a2 | B�� | 6a2 | C�� | 4a3 | D�� | 4a |
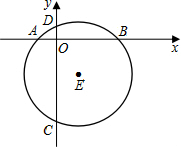 ��ͼ����ֱ������ϵ�У���E�İ뾶Ϊ5����E��1��-4����
��ͼ����ֱ������ϵ�У���E�İ뾶Ϊ5����E��1��-4����