题目内容
15.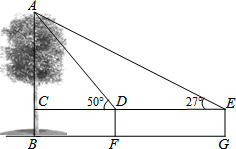 某数学兴趣小组用高为1.2米的测角仪测量小树AB的高度,如图,在距AB一定距离的F处测得小树顶部A的仰角为50°,沿BF方向行走3.5米到G处时,又测得小树顶部A的仰角为27°,求小树AB的高度.(参考数据:sin27°=0.45,cos27°=0.89,tan27°=0.5,sin50°=0.77,cos50°=0.64,tan50°=1.2)
某数学兴趣小组用高为1.2米的测角仪测量小树AB的高度,如图,在距AB一定距离的F处测得小树顶部A的仰角为50°,沿BF方向行走3.5米到G处时,又测得小树顶部A的仰角为27°,求小树AB的高度.(参考数据:sin27°=0.45,cos27°=0.89,tan27°=0.5,sin50°=0.77,cos50°=0.64,tan50°=1.2)
分析 首先设AC=x米,然后由在Rt△ACD中,tan50°=$\frac{AC}{CD}$,求得CD,由在Rt△ACE中,tan27°=$\frac{AC}{CE}$,求得CE,又由CE-CD=DE,即可得方程,继而求得答案.
解答 解:设AC=x米,
在Rt△ACD中,tan50°=$\frac{AC}{CD}$,
∴CD=$\frac{AC}{tan50°}$=$\frac{x}{1.2}$=$\frac{5}{6}$x,
在Rt△ACE中,tan27°=$\frac{AC}{CE}$,
∴CE=$\frac{AC}{tan27°}$=$\frac{x}{0.5}$=2x,
∵CE-CD=DE,
∴2x-$\frac{5}{6}$x=3.5.
解得x=3.
∴AB=AC+CB=3+1.2=4.2(米).
答:小树AB的高为4.2米.
点评 此题考查了仰角的定义.注意能借助仰角构造直角三角形并解直角三角形是解此题的关键.

练习册系列答案
相关题目
7.为了减少燃煤对大气的污染,北京实施煤改电工程.每年冬季采暖季期间可压减燃煤约608000吨,将608000用科学记数法表示应为( )
| A. | 60.8×104 | B. | 6.08×104 | C. | 0.608×106 | D. | 6.08×105 |
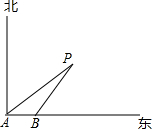 如图,一艘轮船以18海里/时的速度由西向东方向航行,行至A处测得灯塔P在它的北偏东60°的方向上,继续向东行驶20分钟后,到达B处又测得灯塔P在它的北偏东45°方向上,求轮船与灯塔的最短距离.(精确到0.1,$\sqrt{3}$≈1.73)
如图,一艘轮船以18海里/时的速度由西向东方向航行,行至A处测得灯塔P在它的北偏东60°的方向上,继续向东行驶20分钟后,到达B处又测得灯塔P在它的北偏东45°方向上,求轮船与灯塔的最短距离.(精确到0.1,$\sqrt{3}$≈1.73) 如图,直线AB交⊙O于C、D两点,CE是⊙O的直径,CF平分∠ACE交⊙O于点F,连接EF,过点F作FG∥ED交AB于点G.
如图,直线AB交⊙O于C、D两点,CE是⊙O的直径,CF平分∠ACE交⊙O于点F,连接EF,过点F作FG∥ED交AB于点G.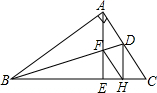 已知,如图,在Rt△ABC中,∠A=90°,AE是高,BD是∠ABC的平分线,AE与BD相交于点F,DH⊥BC,垂足为H,求证:四边形AFHD是菱形.
已知,如图,在Rt△ABC中,∠A=90°,AE是高,BD是∠ABC的平分线,AE与BD相交于点F,DH⊥BC,垂足为H,求证:四边形AFHD是菱形.