题目内容
12.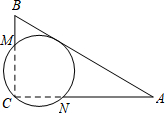 如图,在Rt△ABC中,∠C=90°,AB=13,AC=12,经过点C且与AB边相切的动圆与BC、CA分别相交于点M、N,则线段MN长度的最小值为$\frac{60}{13}$.
如图,在Rt△ABC中,∠C=90°,AB=13,AC=12,经过点C且与AB边相切的动圆与BC、CA分别相交于点M、N,则线段MN长度的最小值为$\frac{60}{13}$.
分析 设MN的中点为P,⊙P与AB的切点为D,连接PD,连接CP,CD,则有PD⊥AB;由勾股定理可求得BC的长,由MN=PD+CP可得到MN≥CD,故此当MN=CD时,MN有最小值,此时点C、P、D在一条直线上,最后利用面积法可求得CD的长,从而得到MN的最小值.
解答 解:如图,设MN的中点为P,⊙P与AB的切点为D,连接PD,连接CP,CD,则有PD⊥AB;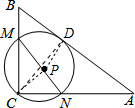
∵AB=13,AC=12,
∴BC=$\sqrt{A{B}^{2}-A{C}^{2}}$=5.
∵PC+PD=MN,
∴PC+PD≥CD,MN≥CD.
∴当MN=CD时,MN有最小值.
∵PD⊥AB,
∴CD⊥AB.
∵$\frac{1}{2}$AB•CD=$\frac{1}{2}$BC•AC,
∴CD=$\frac{BC•AC}{AB}$=$\frac{5×12}{13}$=$\frac{60}{13}$.
∴CD的最小值$\frac{60}{13}$.
∴MN的最小值为$\frac{60}{13}$.
故答案为:$\frac{60}{13}$.
点评 此题主要考查了切线的性质,勾股定理的逆定理,三角形的三边关系,直角三角形的面积公式求解,得出CD=BC•AC÷AB是解题关键.

练习册系列答案
相关题目
17. 如图,将一个边长分别为4、8的矩形纸片ABCD折叠,使点C与点A重合(AB=4,BC=8),则折痕EF的长度为( )
如图,将一个边长分别为4、8的矩形纸片ABCD折叠,使点C与点A重合(AB=4,BC=8),则折痕EF的长度为( )
 如图,将一个边长分别为4、8的矩形纸片ABCD折叠,使点C与点A重合(AB=4,BC=8),则折痕EF的长度为( )
如图,将一个边长分别为4、8的矩形纸片ABCD折叠,使点C与点A重合(AB=4,BC=8),则折痕EF的长度为( )| A. | $\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | $\sqrt{5}$ | D. | 2$\sqrt{5}$ |

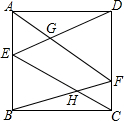 如图,正方形ABCD的面积为4,E,F分别是AB、CD上的点,AF与ED相交于点G,BF与EC相交于点H,求四边形EHFG面积的最大值.
如图,正方形ABCD的面积为4,E,F分别是AB、CD上的点,AF与ED相交于点G,BF与EC相交于点H,求四边形EHFG面积的最大值. 如图,已知△ABC,请用尺规作图,在BC上找一点M,使得AM+MC=BC(保留作图痕迹,不写作法).
如图,已知△ABC,请用尺规作图,在BC上找一点M,使得AM+MC=BC(保留作图痕迹,不写作法).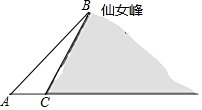 数学“综合与实践”课中,老师带领同学们来到娄底市郊区,测算如图所示的仙女峰的高度,李红盛同学利用已学的数学知识设计了一个实践方案,并实施了如下操作:先在水平地面A处测得山顶B的仰角∠BAC为38.7°,再由A沿水平方向前进377米到达山脚C处,测得山坡BC的坡度为1:0.6,请你求出仙女峰的高度(参考数据:tan38.7°≈0.8)
数学“综合与实践”课中,老师带领同学们来到娄底市郊区,测算如图所示的仙女峰的高度,李红盛同学利用已学的数学知识设计了一个实践方案,并实施了如下操作:先在水平地面A处测得山顶B的仰角∠BAC为38.7°,再由A沿水平方向前进377米到达山脚C处,测得山坡BC的坡度为1:0.6,请你求出仙女峰的高度(参考数据:tan38.7°≈0.8)