题目内容
10.如图,在平行四边形OABC中,∠AOC=60°,OC=4cm,OA=8cm,动点P从点O出发,以1cm/s的速度沿边按O→A→B运动,同时动点Q从点O出发,以1cm/s的速度沿边按O→C→B运动,其中一点到达终点B时,另一点也停止运动,设运动时间为t(s),平行四边形OABC位于直线PQ左侧的图形面积为S(cm2).(1)平行四边形OABC的面积是16$\sqrt{3}$cm2;
(2)当t=6s时,直线PQ平分平行四边形OABC的面积;
(3)求S关于t的函数解析式.

分析 (1)在Rt△COD中求出CD=2$\sqrt{3}$,再利用平行四边形的面积公式即可得出结论;
(2)先求出S梯形OCQP=8$\sqrt{3}$,再用梯形的面积公式即可得出结论;
(3)分三段用三角形和梯形的面积公式即可得出结论.
解答 解:(1)如图1,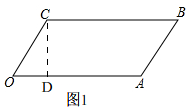
过点C作CD⊥OA于D,
在Rt△COD中,∠AOC=60°,OC=4,
∴CD=2$\sqrt{3}$,
∵OA=8,
∴S平行四边形OABC=OA•CD=8×2$\sqrt{3}$=16$\sqrt{3}$cm2,
故答案为:16$\sqrt{3}$;
(2)如图3,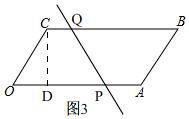 过点C作CD⊥OA于D,
过点C作CD⊥OA于D,
由(1)知,CD=2$\sqrt{3}$,S平行四边形OABC=16$\sqrt{3}$cm2,
∵直线PQ平分平行四边形OABC的面积,
∴S梯形OCQP=$\frac{1}{2}$S平行四边形OABC=$\frac{1}{2}$×16$\sqrt{3}$=8$\sqrt{3}$,
由运动知,CQ=t-4,OP=t,
∴S梯形OCQP=$\frac{1}{2}$(CQ+OP)•CD=$\frac{1}{2}$(t-4+t)×2$\sqrt{3}$=$\sqrt{3}$(2t-4)=8$\sqrt{3}$,
∴t=6,
故答案为:6;
(3)当0≤t≤4时,如图2,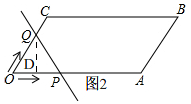
过点Q作QD⊥OA于D,
在Rt△ODQ中,∠AOC=60°,OQ=t,
∴DQ=OQsin∠AOC=$\frac{\sqrt{3}}{2}$t,
∴S=S△OPQ=$\frac{1}{2}$×OP×DQ=$\frac{1}{2}$t×$\frac{\sqrt{3}}{2}$t=$\frac{\sqrt{3}}{4}$t2,
当4<t≤8时,如图3,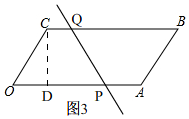
过点C作CD⊥OA于D,
由(1)知,CD=2$\sqrt{3}$,由运动知,CQ=t-4,OP=t,
∴S梯形OCQP=$\frac{1}{2}$(CQ+OP)•CD=$\frac{1}{2}$(t-4+t)×2$\sqrt{3}$=$\sqrt{3}$(2t-4)=2$\sqrt{3}$t-4$\sqrt{3}$,
当8<t≤12时,如图4,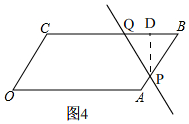 过点P作PD⊥BC于D,
过点P作PD⊥BC于D,
∵四边形OABC时平行四边形,∴∠B=60°,
由运动知,BQ=PB=12-t,
在Rt△PDB中,PD=PBsin∠B=$\frac{\sqrt{3}}{2}$(12-t),
∴S五边形OAPQC=S平行四边形OABC-S△PBQ
=16$\sqrt{3}$-$\frac{1}{2}$BQ×PD=16$\sqrt{3}$-$\frac{1}{2}$(12-t)×$\frac{\sqrt{3}}{2}$(12-t)=16$\sqrt{3}$-$\frac{\sqrt{3}}{4}$(12-t)2,
点评 此题是四边形综合题,主要考查了平行四边形的性质,三角形的面积公式,平行四边形的面积公式,解本题的关键是画出图形,是一道中等难度的中考常考题.

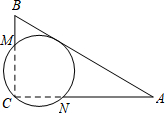 如图,在Rt△ABC中,∠C=90°,AB=13,AC=12,经过点C且与AB边相切的动圆与BC、CA分别相交于点M、N,则线段MN长度的最小值为$\frac{60}{13}$.
如图,在Rt△ABC中,∠C=90°,AB=13,AC=12,经过点C且与AB边相切的动圆与BC、CA分别相交于点M、N,则线段MN长度的最小值为$\frac{60}{13}$.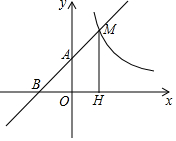 如图,直线y=x+1与x轴交于点B,y轴交于A点,与反比例函数y=$\frac{k}{x}$(x>0)的图象交于点M,过M作MH⊥x轴于点H,且AO=$\frac{1}{2}$MH.
如图,直线y=x+1与x轴交于点B,y轴交于A点,与反比例函数y=$\frac{k}{x}$(x>0)的图象交于点M,过M作MH⊥x轴于点H,且AO=$\frac{1}{2}$MH.
