题目内容
3.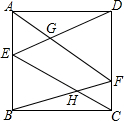 如图,正方形ABCD的面积为4,E,F分别是AB、CD上的点,AF与ED相交于点G,BF与EC相交于点H,求四边形EHFG面积的最大值.
如图,正方形ABCD的面积为4,E,F分别是AB、CD上的点,AF与ED相交于点G,BF与EC相交于点H,求四边形EHFG面积的最大值.
分析 连接EF,作GM⊥AD于M,HN⊥BC于N.设GM=x,HN=y,AE=a,DF=b.想办法证明S四边形GEHF=2(x+y)=[$\frac{ab}{a+b}$+$\frac{(4-a)(4-b)}{8-a-b}$]=2[$\frac{16(a+b)-4({a}^{2}+{b}^{2})}{(a+b)(8-a-b)}$]=4[$\frac{8(a+b)-{a}^{2}-{b}^{2}-({a}^{2}+{b}^{2})}{(a+b)(8-a-b)}$]≤4[$\frac{8(a+b)-{a}^{2}-{b}^{2}-2ab}{(a+b)(8-a-b)}$]=4$\frac{(a+b)(8-a-b)}{(a+b)(8-a-b)}$=4,由此即可解决问题.
解答 解:连接EF,作GM⊥AD于M,HN⊥BC于N.设GM=x,HN=y,AE=a,DF=b.
∵四边形ABCD是正方形,
∴AB∥CD,
∴S△AED=S△AEF,
∴S△AGD=S△AGF,
同理:S△EFH=S△BCH,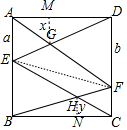
∵S四边形GEHF=S△EFG+S△EFH=S△ADG+S△BCH=$\frac{1}{2}$×4×(x+y)=2(x+y),
∵$\frac{x}{a}$+$\frac{x}{b}$=$\frac{MD}{DA}$+$\frac{AM}{DA}$=1,
∴x=$\frac{ab}{a+b}$,
同理可得y=$\frac{(4-a)(4-b)}{8-a-b}$,
∴S四边形GEHF=2(x+y)=[$\frac{ab}{a+b}$+$\frac{(4-a)(4-b)}{8-a-b}$]
=2[$\frac{16(a+b)-4({a}^{2}+{b}^{2})}{(a+b)(8-a-b)}$]
=4[$\frac{8(a+b)-{a}^{2}-{b}^{2}-({a}^{2}+{b}^{2})}{(a+b)(8-a-b)}$]
≤4[$\frac{8(a+b)-{a}^{2}-{b}^{2}-2ab}{(a+b)(8-a-b)}$]=4$\frac{(a+b)(8-a-b)}{(a+b)(8-a-b)}$=4,
∴四边形EGHF的面积的最大值为4.
点评 本题考查正方形的性质、等高模型、平行线分线段成比例定理、基本不等式等知识,解题的关键是学会利用参数解决问题,属于竞赛题.

 口算题天天练系列答案
口算题天天练系列答案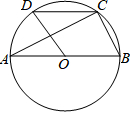 如图,在直径为AB的⊙O中,C,D是⊙O上的两点,∠AOD=58°,CD∥AB,则∠ABC的度数为61°.
如图,在直径为AB的⊙O中,C,D是⊙O上的两点,∠AOD=58°,CD∥AB,则∠ABC的度数为61°.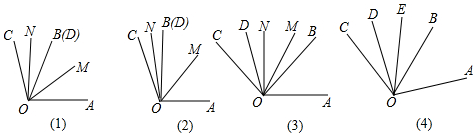
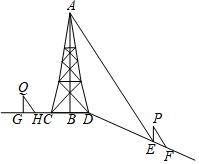 如图,在斜坡顶部有一铁塔AB,B是CD的中点,CD是水平的.在阳光的照射下,塔影DE留在斜坡面上.在同一时刻,小明站在点E处,其影子EF在直线DE上,小华站在点G处,影子GH在直线CD上,他们的影子长分别为2m和1m.已知CD=12m,DE=18m,小明和小华身高均为1.6m,那么塔高AB为多少?
如图,在斜坡顶部有一铁塔AB,B是CD的中点,CD是水平的.在阳光的照射下,塔影DE留在斜坡面上.在同一时刻,小明站在点E处,其影子EF在直线DE上,小华站在点G处,影子GH在直线CD上,他们的影子长分别为2m和1m.已知CD=12m,DE=18m,小明和小华身高均为1.6m,那么塔高AB为多少?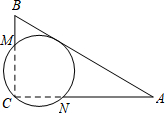 如图,在Rt△ABC中,∠C=90°,AB=13,AC=12,经过点C且与AB边相切的动圆与BC、CA分别相交于点M、N,则线段MN长度的最小值为$\frac{60}{13}$.
如图,在Rt△ABC中,∠C=90°,AB=13,AC=12,经过点C且与AB边相切的动圆与BC、CA分别相交于点M、N,则线段MN长度的最小值为$\frac{60}{13}$.