题目内容
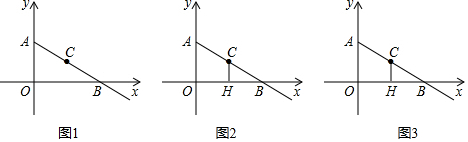
7.如图,四边形ABCD中,AB∥CD,DA⊥AB,CD=20cm,点E为直线AB上一点,过点E作EF∥AD.(1)求证:EF⊥CD;
(2)动点P从点D出发,向点C方向运动,连接EP,判断线段EF与线段EP的大小关系:EP≥EF;
(3)在(2)的条件下,点P运动的同时,有一点Q从点C出发,向点D方向运动,在它们起步的同时,点M从D出发向动点Q运动,遇到点Q后立即返回向点P方向运动,点M如此往返,在P、Q两点之间来回运动,直到P、Q两点相遇后停止,若P、Q两点的速度都为5cm/秒,点M的速度为10cm/秒,连接EM,在点M运动过程中,线段EM扫过的图形面积为100cm2,求EF长.
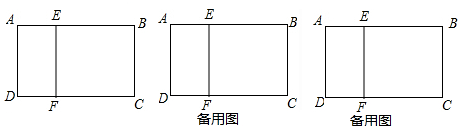
分析 (1)根据矩形的判定定理和性质定理证明;
(2)根据垂线段最短解答;
(3)根据题意求出点M移动的距离,根据三角形的面积公式计算即可.
解答 解:(1)∵AB∥CD,EF∥AD,
∴四边形ADFE是平行四边形,又DA⊥AB,
∴平行四边形ADFE是矩形,
∴EF⊥CD;
(2)∵EF⊥CD,点P在DC上,
∴EP≥EF,
故答案为:≥;
(3)∵CD=20cm,
∴P、Q两点相遇的时间为:$\frac{20}{5+5}$=2s,
则点M移动的距离为:10×2=20cm,
由题意得,$\frac{1}{2}$×EF×20=100,
解得,EF=10cm.
点评 本题考查的是矩形的判定和性质,掌握矩形的判定定理和性质定理、垂线段最短是解题的关键.

练习册系列答案
相关题目