题目内容
14. 如图所示,已知△ABE≌△ACD.
如图所示,已知△ABE≌△ACD.(1)如果BE=6,DE=2,求BC的长;
(2)如果∠BAC=75°,∠BAD=30°,求∠DAE的度数.
分析 (1)根据全等三角形的性质,可得出BE=CD,根据BE=6,DE=2,得出CE=4,从而得出BC的长;
(2)根据全等三角形的性质可得出∠BAE=∠CAD,即可得出∠BAD=∠CAE,计算∠CAD-∠CAE即得出答案.
解答 解:(1)∵△ABE≌△ACD,
∴BE=CD,
∴BE=6,DE=2,
∴CE=4,
∴BC=BE+CE=6+4=10;
(2)∵△ABE≌△ACD,
∴∠BAE=∠CAD,
∵∠BAC=75°,∠BAD=30°,
∴∠BAE=∠CAD=45°,
∴∠DAE=∠CAD-∠CAE=45°-30°=15°.
点评 本题考查了全等三角形的性质,全等三角形的对应边相等,全等三角形的对应角相等.

练习册系列答案
相关题目
3.已知一元二次方程的两根之和是3,两根之积是-2,则这个方程是( )
| A. | x2+3x-2=0 | B. | x2+3x+2=0 | C. | x2-3x+2=0 | D. | x2-3x-2=0 |
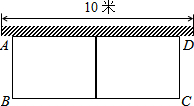 如图所示,有长为24米的篱笆,一面利用墙(墙的最大可用长度为10米)围成中间隔有一道篱笆的矩形花圃,如果花圃的面积为42平方米,求花圃的宽AB.
如图所示,有长为24米的篱笆,一面利用墙(墙的最大可用长度为10米)围成中间隔有一道篱笆的矩形花圃,如果花圃的面积为42平方米,求花圃的宽AB.