题目内容
19．
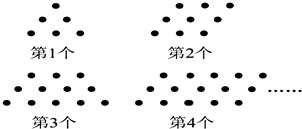用同样大小的黑色棋子按如图的规律摆放：（1）第5个图形有多少颗黑色棋子？
（2）第几个图形有2 016颗黑色棋子？请说明理由．
分析 根据图中所给的黑色棋子的颗数，找出其中的规律，根据规律列出式子，即可求解（1）与（2）．
解答 解：第1个图形有棋子6颗，第2个图形有棋子9颗，第3个图形有棋子12颗，第4个图形有棋子15颗，第5个图形有棋子18颗，…，第n个图形有棋子3（n+1）颗．
（1）第5个图形有18颗黑色棋子；
（2）第n个图形有棋子3（n+1）颗．
设第n个图形有2 016颗黑色棋子，
得3（n+1）=2016，
解得n=671．
所以第671个图形有2016颗黑色棋子．
点评 此题考查了图形的变化类，是一道关于数字猜想的问题，关键是通过归纳与总结，得到其中的规律．
练习册系列答案
相关题目
3．已知一元二次方程的两根之和是3，两根之积是-2，则这个方程是（ ）
| A． | x2+3x-2=0 | B． | x2+3x+2=0 | C． | x2-3x+2=0 | D． | x2-3x-2=0 |
7．
如图，所给的图案由△ABC绕点O顺时针旋转（ ）前后的图形组成的．
如图，所给的图案由△ABC绕点O顺时针旋转（ ）前后的图形组成的．| A． | 45°、90°、135° | B． | 90°、135°、180° | ||
| C． | 45°、90°、135°、180°、225° | D． | 45°、135°、225°、270° |
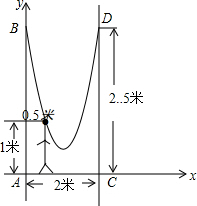如图，小明的父亲在相距2米的两棵树（AB、CD）间拴了一根绳子，给小明做了一个简易的秋千．拴绳子的地方距地面高都是2.5米，绳子自然下垂呈抛物线状，身高1米的小明距较近的那棵树0.5米时，头部刚好接触到绳子．以A为原点，AC所在直线为x轴，AB所在直线为y轴，建立如图所示的直角坐标系．
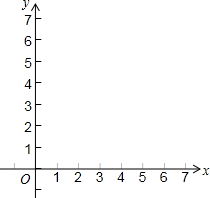（1）在平面直角坐标系中，描出下列各点：（2，1），（6，1），（6，3），（7，3），（4，6），（1，3），（2，3）；
11．3×（-$\frac{1}{3}$）的结果是（ ）
| A． | -4 | B． | -1 | C． | -$\frac{1}{4}$ | D． | $\frac{3}{2}$ |