题目内容
 如图,把长方形纸片ABCD沿EF折叠后,使得点D与点B重合,点C落在点C′的位置上.
如图,把长方形纸片ABCD沿EF折叠后,使得点D与点B重合,点C落在点C′的位置上.(1)折叠后,DC的对应线段是
(2)若∠1=55°,求∠2、∠3的度数;
(3)若AB=3,DE=4,求CF的长度.
考点:翻折变换(折叠问题),勾股定理
专题:
分析:(1)运用翻折变换的定义,即可解决问题.
(2)首先证明∠2=∠1=55°;进而得到∠BEF=∠2=55°,即可解决问题.
(3)首先证明CF=AE,这是解题的关键性结论;求出AE的长,即可解决问题.
(2)首先证明∠2=∠1=55°;进而得到∠BEF=∠2=55°,即可解决问题.
(3)首先证明CF=AE,这是解题的关键性结论;求出AE的长,即可解决问题.
解答: 解:(1)如图,折叠后,DC的对应线段是BC′,
解:(1)如图,折叠后,DC的对应线段是BC′,
CF的对应线段是C′F.
(2)∵四边形ABCD为矩形,
∴DE∥BF,∠2=∠1=55°;
由题意得:∠BEF=∠2=55°,
∴∠3=180°-110°=70°.
(3)∵∠2=∠1,∠BEF=∠2,
∴∠1=∠BEF,BE=BF;而BE=DE=4,
∴BF=DE;而AD=BC,
∴CF=AE;由勾股定理得:AE=
=
,
∴CF=
.
 解:(1)如图,折叠后,DC的对应线段是BC′,
解:(1)如图,折叠后,DC的对应线段是BC′,CF的对应线段是C′F.
(2)∵四边形ABCD为矩形,
∴DE∥BF,∠2=∠1=55°;
由题意得:∠BEF=∠2=55°,
∴∠3=180°-110°=70°.
(3)∵∠2=∠1,∠BEF=∠2,
∴∠1=∠BEF,BE=BF;而BE=DE=4,
∴BF=DE;而AD=BC,
∴CF=AE;由勾股定理得:AE=
| BE2-AB2 |
| 7 |
∴CF=
| 7 |
点评:该题主要考查了翻折变换的性质、勾股定理、等腰三角形的判定等知识点及其应用问题;应牢固掌握翻折变换的性质、勾股定理、等腰三角形的判定等知识点,这是灵活运用解题的基础和关键.

练习册系列答案
相关题目
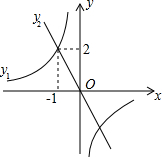 如图,直线y1=k1x与双曲线y2=
如图,直线y1=k1x与双曲线y2=| k2 |
| x |
| A、x<-1 |
| B、0<x<1 |
| C、x<-1或0<x<1 |
| D、-1<x<0或x>1 |
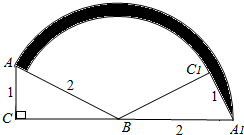 如图所示,△ABC中,∠ACB=90°,AC=1cm,AB=2cm,以B为中心,将△ABC顺时针旋转,使得点A落在边CB延长线上的A1点,此时点C落在点C1,则在旋转中,边AC变到A1C1所扫过的面积为
如图所示,△ABC中,∠ACB=90°,AC=1cm,AB=2cm,以B为中心,将△ABC顺时针旋转,使得点A落在边CB延长线上的A1点,此时点C落在点C1,则在旋转中,边AC变到A1C1所扫过的面积为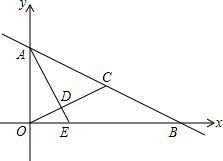 如图,在平面直角坐标系中,点A在y轴上,点B在x轴上,C是线段AB的中点,连接OC,并过点A作OC的垂线,垂足为D,交x轴于点E,已知tan∠OAD=
如图,在平面直角坐标系中,点A在y轴上,点B在x轴上,C是线段AB的中点,连接OC,并过点A作OC的垂线,垂足为D,交x轴于点E,已知tan∠OAD=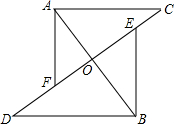 如图,线段AB、CD相交于点O,AC∥DB,AC∥DB,AO=BO,E、F分别为OC、OD的中点,连结AF、BE,求证:AF∥BE.
如图,线段AB、CD相交于点O,AC∥DB,AC∥DB,AO=BO,E、F分别为OC、OD的中点,连结AF、BE,求证:AF∥BE. 如图,在?ABCD中,∠DBC=45°,DE⊥BC于E,BF⊥CD于F,DE、BF 相交于H,BF、AD的延长线相交于G,下面结论:①BD=
如图,在?ABCD中,∠DBC=45°,DE⊥BC于E,BF⊥CD于F,DE、BF 相交于H,BF、AD的延长线相交于G,下面结论:①BD=