题目内容
13.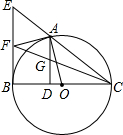 如图,A是以BC为直径的⊙O上的一点,AD⊥BC于点D,过点B作⊙O的切线,与CA的延长线相交于点E,点F是EB的中点,连结CF交AD于点G
如图,A是以BC为直径的⊙O上的一点,AD⊥BC于点D,过点B作⊙O的切线,与CA的延长线相交于点E,点F是EB的中点,连结CF交AD于点G(1)求证:AF是⊙O的切线;
(2)求证:AG=GD;
(3)若FB=FG,且⊙O的半径长为3$\sqrt{2}$,求BD.
分析 (1)要证AF是⊙O的切线,就是要证明∠FAO=90°,连接AB,根据BE是⊙O的切线和直角三角形的等量代换,就可得出结论;
(2)根据切线判定知道EB⊥BC,而AD⊥BC,从而可以确定AD∥BE,那么△BFC∽△DGC,又点F是EB的中点,就可得出结论;
(3)点F作FH⊥AD于点H,根据前两问的结论,利用三角形的相似性和勾股定理,可以求出BD的长度.
解答 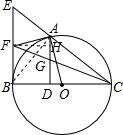 (1)证明:连结AB,
(1)证明:连结AB,
∵BC是⊙O的直径,
∴∠BAC=90°.
∵F是斜边BE的中点,
∴AF=FB=EF,
∴∠FBA=∠FAB,
又∵OA=OB,
∴∠ABO=∠BAO
∵BE是⊙O的切线,
∴∠EBO=90°
∵∠EBO=∠FBA+∠ABO=∠FAB+∠BAO=∠FAO=90°
∴AF是⊙O的切线;
(2)证明:∵BC是⊙O的直径,BE是⊙O的切线,
∴EB⊥BC.
又∵AD⊥BC,
∴AD∥BE,
∴△BFC∽△DGC,△FEC∽△GAC,
∴$\frac{BF}{DG}$=$\frac{CF}{CG}$,$\frac{EF}{AG}$=$\frac{CF}{CG}$,
∴$\frac{BF}{DG}$=$\frac{EF}{AG}$,
∵F是斜边BE的中点,
∴BF=EF,
∴DG=AG;
(3)解:过点F作FH⊥AD于点H,
∵BD⊥AD,FH⊥AD,
∴FH∥BC.
由(2),知∠FBA=∠BAF,
∴BF=AF.
由已知,有BF=FG,
∴AF=FG,即△AFG是等腰三角形.
∵FH⊥AD,
∴AH=GH,
∵DG=AG,
∴DG=2HG,
即$\frac{HG}{DG}$=$\frac{1}{2}$,
∵FH∥BD,BF∥AD,∠FBD=90°,
∴四边形BDHF是矩形,BD=FH,
∵FH∥BC,易证△HFG∽△DCG,
∴$\frac{FH}{CD}$=$\frac{FG}{CG}$=$\frac{HG}{DG}$,
即$\frac{BD}{CD}$=$\frac{FG}{CG}$=$\frac{HG}{DG}$=$\frac{1}{2}$.
∵⊙O的半径长为3$\sqrt{2}$,
∴BC=6$\sqrt{2}$.
∴$\frac{BD}{CD}$=$\frac{BD}{BC-BD}$=$\frac{BD}{BD-6\sqrt{2}}$=$\frac{1}{2}$,
解得BD=2$\sqrt{2}$.
∴BD=FH=2$\sqrt{2}$.
点评 本题考查的是切线的判定和性质,相似三角形的判定和性质,矩形的判定和性质,要证某线是圆的切线,已知此线过圆上某点,连接圆心和这点(即为半径),再证垂直即可.

 下列条件不能够证明a∥b的是( )
下列条件不能够证明a∥b的是( )| A. | ∠2+∠3=180° | B. | ∠1=∠4 | C. | ∠2+∠4=180° | D. | ∠2=∠3 |
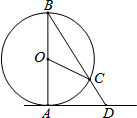 如图,AD是⊙O的切线,A为切点.点C在⊙O上,连接BC并延长交AD于点D,若∠AOC=70°,则∠ADB=( )
如图,AD是⊙O的切线,A为切点.点C在⊙O上,连接BC并延长交AD于点D,若∠AOC=70°,则∠ADB=( )| A. | 35° | B. | 45° | C. | 55° | D. | 65° |
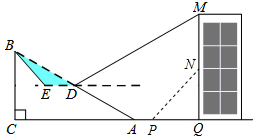 如图,斜坡AB长130米,坡度i=1:2.4,BC⊥AC,现计划在斜坡中点D处挖去部分坡体修建一个平行于水平线CA的平台DE和一条新的斜坡BE.
如图,斜坡AB长130米,坡度i=1:2.4,BC⊥AC,现计划在斜坡中点D处挖去部分坡体修建一个平行于水平线CA的平台DE和一条新的斜坡BE.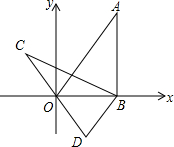 如图,在平面直角坐标系xOy中,直线y=$\sqrt{3}$x经过点A,作AB⊥x轴于点B,将△ABO绕点B逆时针旋转60°得到△CBD,若点B的坐标为(2,0),则点C的坐标为(-1,$\sqrt{3}$).
如图,在平面直角坐标系xOy中,直线y=$\sqrt{3}$x经过点A,作AB⊥x轴于点B,将△ABO绕点B逆时针旋转60°得到△CBD,若点B的坐标为(2,0),则点C的坐标为(-1,$\sqrt{3}$).