题目内容
1.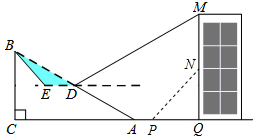 如图,斜坡AB长130米,坡度i=1:2.4,BC⊥AC,现计划在斜坡中点D处挖去部分坡体修建一个平行于水平线CA的平台DE和一条新的斜坡BE.
如图,斜坡AB长130米,坡度i=1:2.4,BC⊥AC,现计划在斜坡中点D处挖去部分坡体修建一个平行于水平线CA的平台DE和一条新的斜坡BE.(1)若修建的斜坡BE的坡角为30°,求平台DE的长.(结果保留根号).
(2)斜坡AB正前方一座建筑物QM上悬挂了一幅巨型广告MN,小明在D点测得广告顶部M的仰角为26.5°,他沿坡面DA走到坡脚A处,然后向大楼方向维续行走10米来到P处,测得广告底部N的仰角为53°,此时小明距大楼底端Q处30米.已知B、C、A、M、Q在同一平面内,C、A、P、Q在同一条直线上,求广告MN的长度.(参考数据:sin26.5°≈0.45,cos26.5°=0.89,tan26.5°=0.50,sin53°≈0.80,cos53°≈0.60,tan53°≈1.33°)
分析 (1)如图延长DE交BC于F,根据坡度的定义设BC=5k,AC=12k,利用勾股定理求出BC、AC,利用三角形中位线定理求出DF,在RT△BEF中求出EF即可解决问题.
(2)延长ED交MQ于H,则四边形CFHQ是矩形,在RT△DHM中求出HM,在RT△PNQ中求出NQ即可解决问题.
解答 解:(1)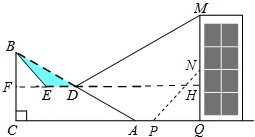 如图延长DE交BC于F.
如图延长DE交BC于F.
∵i=$\frac{BC}{AC}$=$\frac{1}{2.4}$=$\frac{5}{12}$,
设BC=5k,AC=12k.
在RT△ABC中,∵∠C=90°,AB=130,
∴(5k)2+(12K)2=1302,
∴k=10(负根以及舍弃).
∴BC=50米,AC=120米.
∵BD=DA,DF∥AC,
∴BF=FC=25米,DF=$\frac{1}{2}$AC=60米,
在RT△BEF中,∵∠BFE=90°,∠BEF=30°,
∴BE=2BF=50,EF=$\sqrt{3}$FB=25$\sqrt{3}$米,
∴DE=DF-EF=(60-25$\sqrt{3}$)米.
(2)延长ED交MQ于H,则四边形CFHQ是矩形,CF=HQ=25米,FH=CQ=160米
在RT△DHM中,∵∠DHM=90°,DH=FH-DF=CQ-DF=160-60=100,
∴MH=DH•tan26.5°≈50,MQ=HM+HQ=75,
在RT△PNQ中,∵∠PQN=90°,PQ=30,
∴NQ=PQ•tan53°≈40,
∴MN=MQ-NQ=75-40=35米.
点评 本题考查解直角三角形、坡度、坡角、仰角、勾股定理、三角函数等知识,熟练掌握这些知识就解决问题的关键,属于中考常考题型.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
11.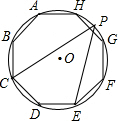 如图,正八边形ABCDEFGH内接于圆,点P是弧GH上的任意一点,则∠CPE的度数为( )
如图,正八边形ABCDEFGH内接于圆,点P是弧GH上的任意一点,则∠CPE的度数为( )
 如图,正八边形ABCDEFGH内接于圆,点P是弧GH上的任意一点,则∠CPE的度数为( )
如图,正八边形ABCDEFGH内接于圆,点P是弧GH上的任意一点,则∠CPE的度数为( )| A. | 30° | B. | 15° | C. | 60° | D. | 45° |
8.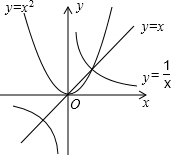 给出下列命题及函数y=x,y=x2和y=$\frac{1}{x}$的图象:
给出下列命题及函数y=x,y=x2和y=$\frac{1}{x}$的图象:
①如果$\frac{1}{a}$>a>a2,那么0<a<1;
②如果a2>a>$\frac{1}{a}$,那么a>1;
③如果$\frac{1}{a}$>a2>a,那么-1<a<0;
④如果a2>$\frac{1}{a}$>a,那么a<-1.
 给出下列命题及函数y=x,y=x2和y=$\frac{1}{x}$的图象:
给出下列命题及函数y=x,y=x2和y=$\frac{1}{x}$的图象:①如果$\frac{1}{a}$>a>a2,那么0<a<1;
②如果a2>a>$\frac{1}{a}$,那么a>1;
③如果$\frac{1}{a}$>a2>a,那么-1<a<0;
④如果a2>$\frac{1}{a}$>a,那么a<-1.
| A. | 正确的命题是①② | B. | 错误的命题是②③④ | C. | 正确的命题是①④ | D. | 错误的命题只有③ |
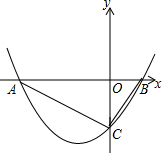 如图,已知抛物线y=$\frac{1}{2}$x2+bx+c与x轴交于A(-4,0),B(1,0)两点,与y轴交于C点,则△ABC的面积是5.
如图,已知抛物线y=$\frac{1}{2}$x2+bx+c与x轴交于A(-4,0),B(1,0)两点,与y轴交于C点,则△ABC的面积是5.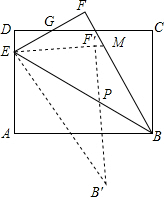 如图,矩形ABCD中,AB=10,BC=7.5,点E是AD上一点,把△ABE沿BE翻折至△FBE,EF与DC相交于点G且DG=FG,再把△FBE绕点E顺时针旋转一定的角度α(0°<α<90°)后得到△F′EB′,EF′的延长线交BF于点M,EB′交AB于点N,当ME=MB时,AN的长度是$\frac{18}{5}$.
如图,矩形ABCD中,AB=10,BC=7.5,点E是AD上一点,把△ABE沿BE翻折至△FBE,EF与DC相交于点G且DG=FG,再把△FBE绕点E顺时针旋转一定的角度α(0°<α<90°)后得到△F′EB′,EF′的延长线交BF于点M,EB′交AB于点N,当ME=MB时,AN的长度是$\frac{18}{5}$.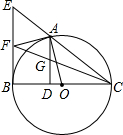 如图,A是以BC为直径的⊙O上的一点,AD⊥BC于点D,过点B作⊙O的切线,与CA的延长线相交于点E,点F是EB的中点,连结CF交AD于点G
如图,A是以BC为直径的⊙O上的一点,AD⊥BC于点D,过点B作⊙O的切线,与CA的延长线相交于点E,点F是EB的中点,连结CF交AD于点G