题目内容
20.计算:$\sqrt{2}$-tan60°+2-1-|-$\sqrt{3}$|分析 原式第二项利用特殊角的三角函数值计算,第三项利用负整数指数幂法则计算,最后一项利用绝对值的代数意义化简,计算即可得到结果.
解答 解:原式=$\sqrt{2}$-$\sqrt{3}$+$\frac{1}{2}$-$\sqrt{3}$=$\sqrt{2}$-2$\sqrt{3}$+$\frac{1}{2}$.
点评 此题考查了实数的运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
11.若关于x的一元二次方程x2-4x+(5-m)=0有实数根,则m的取值范围是( )
| A. | m>1 | B. | m≥1 | C. | m<1 | D. | m≤1 |
8.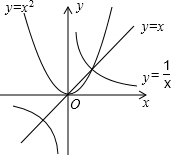 给出下列命题及函数y=x,y=x2和y=$\frac{1}{x}$的图象:
给出下列命题及函数y=x,y=x2和y=$\frac{1}{x}$的图象:
①如果$\frac{1}{a}$>a>a2,那么0<a<1;
②如果a2>a>$\frac{1}{a}$,那么a>1;
③如果$\frac{1}{a}$>a2>a,那么-1<a<0;
④如果a2>$\frac{1}{a}$>a,那么a<-1.
 给出下列命题及函数y=x,y=x2和y=$\frac{1}{x}$的图象:
给出下列命题及函数y=x,y=x2和y=$\frac{1}{x}$的图象:①如果$\frac{1}{a}$>a>a2,那么0<a<1;
②如果a2>a>$\frac{1}{a}$,那么a>1;
③如果$\frac{1}{a}$>a2>a,那么-1<a<0;
④如果a2>$\frac{1}{a}$>a,那么a<-1.
| A. | 正确的命题是①② | B. | 错误的命题是②③④ | C. | 正确的命题是①④ | D. | 错误的命题只有③ |
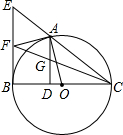 如图,A是以BC为直径的⊙O上的一点,AD⊥BC于点D,过点B作⊙O的切线,与CA的延长线相交于点E,点F是EB的中点,连结CF交AD于点G
如图,A是以BC为直径的⊙O上的一点,AD⊥BC于点D,过点B作⊙O的切线,与CA的延长线相交于点E,点F是EB的中点,连结CF交AD于点G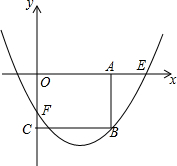 如图,在平面直角坐标系中,抛物线y=$\frac{1}{a}{x}^{2}-\frac{4}{a}x-a$(a>0)与x轴正半轴交于点E,与y轴交于点F,过点A(2a,0)作AB∥y轴,交抛物线于点B,过点B作BC⊥y轴于点C.
如图,在平面直角坐标系中,抛物线y=$\frac{1}{a}{x}^{2}-\frac{4}{a}x-a$(a>0)与x轴正半轴交于点E,与y轴交于点F,过点A(2a,0)作AB∥y轴,交抛物线于点B,过点B作BC⊥y轴于点C.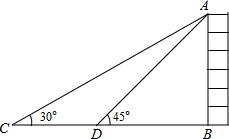 如图,如果在大厦AB所在的平地上选择一点C,测得大厦顶端A的仰角为30°,然后向大厦方向前进40米,到达点D处(C、D、B三点在同一直线上),此时测得大厦顶端A的仰角为45°,那么大厦AB的高度为20$\sqrt{3}$+20米(保留根号).
如图,如果在大厦AB所在的平地上选择一点C,测得大厦顶端A的仰角为30°,然后向大厦方向前进40米,到达点D处(C、D、B三点在同一直线上),此时测得大厦顶端A的仰角为45°,那么大厦AB的高度为20$\sqrt{3}$+20米(保留根号).