题目内容
8.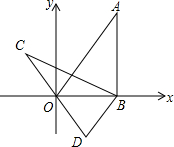 如图,在平面直角坐标系xOy中,直线y=$\sqrt{3}$x经过点A,作AB⊥x轴于点B,将△ABO绕点B逆时针旋转60°得到△CBD,若点B的坐标为(2,0),则点C的坐标为(-1,$\sqrt{3}$).
如图,在平面直角坐标系xOy中,直线y=$\sqrt{3}$x经过点A,作AB⊥x轴于点B,将△ABO绕点B逆时针旋转60°得到△CBD,若点B的坐标为(2,0),则点C的坐标为(-1,$\sqrt{3}$).
分析 在RT△AOB中,求出AO的长,根据旋转的性质可得AO=CD=4、OB=BD、△OBD是等边三角形,进而可得RT△COE中∠COE=60°、CO=2,由三角函数可得OE、CE.
解答 解:过点C作CE⊥x轴于点E,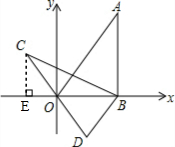
∵OB=2,AB⊥x轴,点A在直线y=$\sqrt{3}$x上,
∴AB=2$\sqrt{3}$,OA=$\sqrt{O{B}^{2}+A{B}^{2}}$=4,
∴RT△ABO中,tan∠AOB=$\frac{2\sqrt{3}}{2}$=$\sqrt{3}$,
∴∠AOB=60°,
又∵△CBD是由△ABO绕点B逆时针旋转60°得到,
∴∠D=∠AOB=∠OBD=60°,AO=CD=4,
∴△OBD是等边三角形,
∴DO=OB=2,∠DOB=∠COE=60°,
∴CO=CD-DO=2,
在RT△COE中,OE=CO•cos∠COE=2×$\frac{1}{2}$=1,
CE=CO•sin∠COE=2×$\frac{\sqrt{3}}{2}$=$\sqrt{3}$,
∴点C的坐标为(-1,$\sqrt{3}$),
故答案为:(-1,$\sqrt{3}$).
点评 本题主要考查在旋转的情况下点的坐标变化,熟知旋转过程中图形全等即对应边相等、对应角相等、旋转角都相等的应用是解题的切入点也是关键.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
3.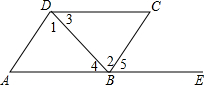 如图,点A,B,E在一条直线上,下列条件中不能判断AD∥BC的是( )
如图,点A,B,E在一条直线上,下列条件中不能判断AD∥BC的是( )
 如图,点A,B,E在一条直线上,下列条件中不能判断AD∥BC的是( )
如图,点A,B,E在一条直线上,下列条件中不能判断AD∥BC的是( )| A. | ∠1=∠2 | B. | ∠A+∠ABC=180° | C. | ∠A=∠5 | D. | ∠3=∠4 |
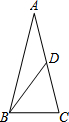 如图,在△ABC中,AB=AC=4,cosC=$\frac{1}{4}$,BD是中线,将△CBD沿直线BD翻折后,点C落在点E,那么AE的长为$\sqrt{6}$.
如图,在△ABC中,AB=AC=4,cosC=$\frac{1}{4}$,BD是中线,将△CBD沿直线BD翻折后,点C落在点E,那么AE的长为$\sqrt{6}$.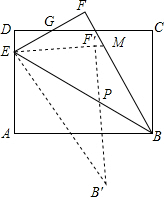 如图,矩形ABCD中,AB=10,BC=7.5,点E是AD上一点,把△ABE沿BE翻折至△FBE,EF与DC相交于点G且DG=FG,再把△FBE绕点E顺时针旋转一定的角度α(0°<α<90°)后得到△F′EB′,EF′的延长线交BF于点M,EB′交AB于点N,当ME=MB时,AN的长度是$\frac{18}{5}$.
如图,矩形ABCD中,AB=10,BC=7.5,点E是AD上一点,把△ABE沿BE翻折至△FBE,EF与DC相交于点G且DG=FG,再把△FBE绕点E顺时针旋转一定的角度α(0°<α<90°)后得到△F′EB′,EF′的延长线交BF于点M,EB′交AB于点N,当ME=MB时,AN的长度是$\frac{18}{5}$.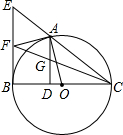 如图,A是以BC为直径的⊙O上的一点,AD⊥BC于点D,过点B作⊙O的切线,与CA的延长线相交于点E,点F是EB的中点,连结CF交AD于点G
如图,A是以BC为直径的⊙O上的一点,AD⊥BC于点D,过点B作⊙O的切线,与CA的延长线相交于点E,点F是EB的中点,连结CF交AD于点G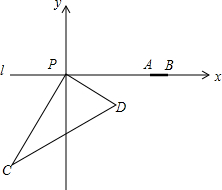 如图,在东西方向的海岸线l有一长为2km的码头AB,在码头的西端A的正西29km处有一观测站P,某时刻测得一艘匀速直线航行的轮船位于P的南偏西30°,且与P相距30km的C处;经过1小时40分钟,又测得该轮船位于P的南偏东60°,且与P相距10$\sqrt{3}$的D处.
如图,在东西方向的海岸线l有一长为2km的码头AB,在码头的西端A的正西29km处有一观测站P,某时刻测得一艘匀速直线航行的轮船位于P的南偏西30°,且与P相距30km的C处;经过1小时40分钟,又测得该轮船位于P的南偏东60°,且与P相距10$\sqrt{3}$的D处.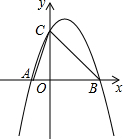 已知抛物线y=-x2+2x+3与x轴交于A,B两点,其中A点位于B点的左侧,与y轴交于点C,顶点为P,则:
已知抛物线y=-x2+2x+3与x轴交于A,B两点,其中A点位于B点的左侧,与y轴交于点C,顶点为P,则: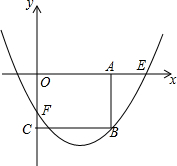 如图,在平面直角坐标系中,抛物线y=$\frac{1}{a}{x}^{2}-\frac{4}{a}x-a$(a>0)与x轴正半轴交于点E,与y轴交于点F,过点A(2a,0)作AB∥y轴,交抛物线于点B,过点B作BC⊥y轴于点C.
如图,在平面直角坐标系中,抛物线y=$\frac{1}{a}{x}^{2}-\frac{4}{a}x-a$(a>0)与x轴正半轴交于点E,与y轴交于点F,过点A(2a,0)作AB∥y轴,交抛物线于点B,过点B作BC⊥y轴于点C.