题目内容
18．
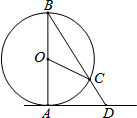如图，AD是⊙O的切线，A为切点．点C在⊙O上，连接BC并延长交AD于点D，若∠AOC=70°，则∠ADB=（ ）| A． | 35° | B． | 45° | C． | 55° | D． | 65° |
分析 先证明△ABD是直角三角形，求出∠B即可解决问题．
解答 解：∵OB=OC，∠AOC=70°，∠AOC=∠B+∠OCB，
∴∠B=∠OCB=35°，
∵AD是⊙O的切线，
∴AB⊥AD，
∴∠BAD=90°，
∴∠ADB=90°-∠B=55°．
故选C．
点评 本题考查了切线的性质，等腰三角形的性质、直角三角形两锐角互余等知识，利用切线垂直于过切点的半径是解题的关键，学会用转化的思想去思考问题，属于中考常考题型．
练习册系列答案
口算能手系列答案
相关题目
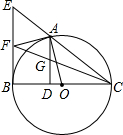如图，A是以BC为直径的⊙O上的一点，AD⊥BC于点D，过点B作⊙O的切线，与CA的延长线相交于点E，点F是EB的中点，连结CF交AD于点G
4．
某超市举行购物“翻牌抽奖”活动，如图所示，四张牌分别对应价值5，10，15，20（单位：元）的四件奖品，如果随机翻两张牌，且第一次翻过的牌不再参加下次翻牌，则所获奖品总价值不低于30元的概率为（ ）
某超市举行购物“翻牌抽奖”活动，如图所示，四张牌分别对应价值5，10，15，20（单位：元）的四件奖品，如果随机翻两张牌，且第一次翻过的牌不再参加下次翻牌，则所获奖品总价值不低于30元的概率为（ ）| A． | $\frac{1}{2}$ | B． | $\frac{2}{3}$ | C． | $\frac{1}{3}$ | D． | $\frac{3}{4}$ |