题目内容
10．
如图，分别以五边形ABCDE的顶点为圆心，以1为半径作五个圆，则图中阴影部分的面积之和为（ ）| A． | $\frac{3}{2}π$ | B． | 3π | C． | $\frac{7}{2}π$ | D． | 2π |
分析 圆心角之和等于n边形的内角和（n-2）×180°，由于半径相同，根据扇形的面积公式S=$\frac{nπ{r}^{2}}{360}$计算即可求出圆形中的空白面积，再用5个圆形的面积减去圆形中的空白面积可得阴影部分的面积．
解答 解：n边形的内角和（n-2）×180°，
圆形的空白部分的面积之和S=$\frac{180（n-2）π×{1}^{2}}{360}$=$\frac{n-2}{2}$π=$\frac{5-2}{2}$π=$\frac{3}{2}$π．
所以图中阴影部分的面积之和为：5πr2-$\frac{3}{2}$π=5π-$\frac{3}{2}$π=$\frac{7}{2}$π．
故选：C．
点评 此题考查扇形的面积计算，正确记忆多边形的内角和公式，以及扇形的面积公式是解决本题的关键．
练习册系列答案
世纪百通期末金卷系列答案
相关题目
20．
如图，△ABC内接于直径为d的圆，AC=b，BC=a，则△ABC的高CD为（ ）
如图，△ABC内接于直径为d的圆，AC=b，BC=a，则△ABC的高CD为（ ）| A． | $\frac{2ab}{d}$ | B． | $\frac{bd}{a}$ | C． | $\frac{ad}{b}$ | D． | $\frac{ab}{d}$ |
1．若abc≠0，且a，b，c满足方程组$\left\{{\begin{array}{l}{5a+2b-9c=0}\\{4a-3b+2c=0}\end{array}}\right.$，则$\frac{5a-b+7c}{3a+2b+3c}$=（ ）
| A． | -1 | B． | 1 | C． | $-\frac{11}{8}$ | D． | $\frac{11}{8}$ |
18．如果（x2-mx-n）（x-3）的乘积中不含x2项和x项，那么（ ）
| A． | m=0，n=0 | B． | m=-3，n=-9 | C． | m=-3，n=9 | D． | m=3，n=-9 |
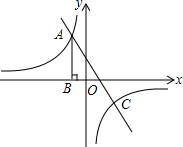如图，反比例函数y=$\frac{k}{x}$的图象经过第二象限内的点A，AB⊥x轴于点B，OB=1，AB=4．