题目内容
18. 如图,在?ABCD中,E、F分别是AD、CD边上的点,连接BE、AF,它们相交于点G,延长BE交CD的延长线于点H,下列结论错误的是( )
如图,在?ABCD中,E、F分别是AD、CD边上的点,连接BE、AF,它们相交于点G,延长BE交CD的延长线于点H,下列结论错误的是( )| A. | $\frac{AE}{ED}=\frac{BE}{EH}$ | B. | $\frac{EH}{EB}=\frac{DH}{CD}$ | C. | $\frac{EG}{BG}=\frac{AE}{BC}$ | D. | $\frac{AG}{FG}=\frac{BG}{GH}$ |
分析 由平行四边形的性质得出AB∥CD,AD∥BC,证出△ABE∽△DHE,△ABG∽△FHG,$\frac{EH}{EB}=\frac{DH}{CD}$,得出对应边成比例$\frac{AE}{ED}=\frac{BE}{EH}$,$\frac{AG}{FG}=\frac{BG}{GH}$,即可得出结论.
解答 解:∵四边形ABCD是平行四边形,
∴AB∥CD,AD∥BC,
∴△ABE∽△DHE,△ABG∽△FHG,$\frac{EH}{EB}=\frac{DH}{CD}$,
∴$\frac{AE}{ED}=\frac{BE}{EH}$,$\frac{AG}{FG}=\frac{BG}{GH}$,
∴选项A、B、D正确,C错误;
故选:C.
点评 本题考查了平行四边形的性质、相似三角形的判定与性质、平行线分线段成比例定理;熟练掌握平行四边形的性质是解决问题的关键.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案
相关题目
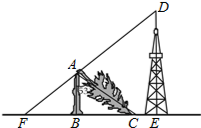 如图,一棵大树在一次强台风中折断倒下,未折断树杆AB与地面仍保持垂直的关系,而折断部分AC与未折断树杆AB形成53°的夹角.树杆AB旁有一座与地面垂直的铁塔DE,测得BE=6米,塔高DE=9米.在某一时刻的太阳照射下,未折断树杆AB落在地面的影子FB长为4米,且点F、B、C、E在同一条直线上,点F、A、D也在同一条直线上.求这棵大树没有折断前的高度.(参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈1.33)
如图,一棵大树在一次强台风中折断倒下,未折断树杆AB与地面仍保持垂直的关系,而折断部分AC与未折断树杆AB形成53°的夹角.树杆AB旁有一座与地面垂直的铁塔DE,测得BE=6米,塔高DE=9米.在某一时刻的太阳照射下,未折断树杆AB落在地面的影子FB长为4米,且点F、B、C、E在同一条直线上,点F、A、D也在同一条直线上.求这棵大树没有折断前的高度.(参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈1.33) 将含有30°角的直角三角板的直角顶点放在平行的两条直线的一条直线上,若∠2=23°,则∠1的度数是37°.
将含有30°角的直角三角板的直角顶点放在平行的两条直线的一条直线上,若∠2=23°,则∠1的度数是37°.