题目内容
3.不透明的布袋里有2个红色小汽车,2个白色小汽车模型(小汽车除颜色不同外,其它都相同),从布袋中随机摸出1个小汽车记下颜色后放回袋中摇匀,然后重新再摸出1个小汽车,则摸出的两个小汽车都是红色的概率是$\frac{1}{4}$.分析 列出表格,然后根据概率公式列式计算即可得解.
解答 解:
解:分别用红1、红2代表2个红色小汽车模型,白1、白2代表2个白色小汽车模型,
根据题意,列表如下:
| 红1 | 红2 | 白1 | 白2 | |
| 红1 | (红1,红1) | (红1,红2) | (红1,白1) | (红1,白2) |
| 红2 | (红2,红1) | (红2,红2) | (红2,白1) | (红2,白2) |
| 白1 | (白1,红1) | (白1,红2) | (白1,白1) | (白1,白2) |
| 白2 | (白2,红1) | (白2,红2) | (白2,白1) | (白2,白2) |
∴摸出的两个小汽车都是红色的概率$\frac{4}{16}$=$\frac{1}{4}$.
故答案为:$\frac{1}{4}$.
点评 本题考查的是用列表法或画树状图法求概率.列表法或画树状图法可以不重复不遗漏的列出所有可能的结果,列表法适合于两步完成的事件,树状图法适合两步或两步以上完成的事件,注意是否是放回还是不放回事件是解题的关键.

练习册系列答案
相关题目
13.若关于x的不等式组$\left\{\begin{array}{l}{x<2}\\{x-a≥0}\end{array}\right.$的整数解共有5个,则a的取值范围是( )
| A. | -4<a≤-3 | B. | -4≤a<-3 | C. | -4≤a≤-3 | D. | -4<a<-3 |
18. 如图,在?ABCD中,E、F分别是AD、CD边上的点,连接BE、AF,它们相交于点G,延长BE交CD的延长线于点H,下列结论错误的是( )
如图,在?ABCD中,E、F分别是AD、CD边上的点,连接BE、AF,它们相交于点G,延长BE交CD的延长线于点H,下列结论错误的是( )
 如图,在?ABCD中,E、F分别是AD、CD边上的点,连接BE、AF,它们相交于点G,延长BE交CD的延长线于点H,下列结论错误的是( )
如图,在?ABCD中,E、F分别是AD、CD边上的点,连接BE、AF,它们相交于点G,延长BE交CD的延长线于点H,下列结论错误的是( )| A. | $\frac{AE}{ED}=\frac{BE}{EH}$ | B. | $\frac{EH}{EB}=\frac{DH}{CD}$ | C. | $\frac{EG}{BG}=\frac{AE}{BC}$ | D. | $\frac{AG}{FG}=\frac{BG}{GH}$ |
8.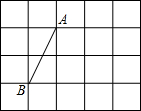 如图,A、B两点均在由小正方形组成的网格格点上,若C点也在格点上,且△ABC是等腰直角三角形,则符合条件的C点的个数有( )
如图,A、B两点均在由小正方形组成的网格格点上,若C点也在格点上,且△ABC是等腰直角三角形,则符合条件的C点的个数有( )
 如图,A、B两点均在由小正方形组成的网格格点上,若C点也在格点上,且△ABC是等腰直角三角形,则符合条件的C点的个数有( )
如图,A、B两点均在由小正方形组成的网格格点上,若C点也在格点上,且△ABC是等腰直角三角形,则符合条件的C点的个数有( )| A. | 3个 | B. | 4个 | C. | 5个 | D. | 6个 |
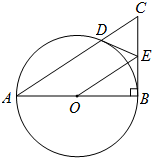 如图,以Rt△ABC的直角边AB为直径作⊙O与斜边AC交于点D,E为BC边的中点,连接DE,OE.
如图,以Rt△ABC的直角边AB为直径作⊙O与斜边AC交于点D,E为BC边的中点,连接DE,OE.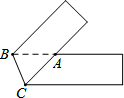 将一张宽为5cm的长方形纸片(足够长)折叠成如图所示图形,重叠部分是一个三角形,则这个三角形面积的最小值是$\frac{25}{2}$cm2.
将一张宽为5cm的长方形纸片(足够长)折叠成如图所示图形,重叠部分是一个三角形,则这个三角形面积的最小值是$\frac{25}{2}$cm2.