题目内容
20.解下列方程:(1)x2+4x-3=0;
(2)7(x+3)=2x(x+3).
分析 (1)利用配方法求得方程的解即可;
(2)利用因式分解法求得方程的解即可.
解答 解:(1)x2+4x-3=0
(x+2)2=7
x+2=±$\sqrt{7}$
解得:x1=-$\sqrt{7}$-2,x2=$\sqrt{7}$-2;
(2)7(x+3)=2x(x+3)
(x+3)(7-2x)=0
x+3=0,7-2x=0
解得:x1=-3,x2=$\frac{7}{2}$.
点评 此题考查解一元二次方程,掌握配方法、因式分解法解方程的步骤与方法是解决问题的关键.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
10.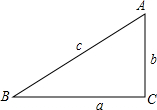 如图,在Rt△ABC中,∠C=90°,∠A、∠B、∠C所对的边分别用a、b、c表示,我们定义:锐角∠A的对边a与斜边c的比值$\frac{a}{c}$叫做∠A的正弦值,记为:sinA=$\frac{a}{c}$.如果某个直角三角形中,a=4,c=5,则∠A的正弦值为$\frac{4}{5}$,记为:sinA=$\frac{4}{5}$.如果某直角三角形中,∠A=60°,则sinA是( )
如图,在Rt△ABC中,∠C=90°,∠A、∠B、∠C所对的边分别用a、b、c表示,我们定义:锐角∠A的对边a与斜边c的比值$\frac{a}{c}$叫做∠A的正弦值,记为:sinA=$\frac{a}{c}$.如果某个直角三角形中,a=4,c=5,则∠A的正弦值为$\frac{4}{5}$,记为:sinA=$\frac{4}{5}$.如果某直角三角形中,∠A=60°,则sinA是( )
 如图,在Rt△ABC中,∠C=90°,∠A、∠B、∠C所对的边分别用a、b、c表示,我们定义:锐角∠A的对边a与斜边c的比值$\frac{a}{c}$叫做∠A的正弦值,记为:sinA=$\frac{a}{c}$.如果某个直角三角形中,a=4,c=5,则∠A的正弦值为$\frac{4}{5}$,记为:sinA=$\frac{4}{5}$.如果某直角三角形中,∠A=60°,则sinA是( )
如图,在Rt△ABC中,∠C=90°,∠A、∠B、∠C所对的边分别用a、b、c表示,我们定义:锐角∠A的对边a与斜边c的比值$\frac{a}{c}$叫做∠A的正弦值,记为:sinA=$\frac{a}{c}$.如果某个直角三角形中,a=4,c=5,则∠A的正弦值为$\frac{4}{5}$,记为:sinA=$\frac{4}{5}$.如果某直角三角形中,∠A=60°,则sinA是( )| A. | 1 | B. | 0 | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
11.下列几组数中,是勾股数的有( )
①0.6,0.8,1;②5,12,13;③6,8,10;④$\frac{1}{3}$,$\frac{1}{4}$,$\frac{1}{5}$.
①0.6,0.8,1;②5,12,13;③6,8,10;④$\frac{1}{3}$,$\frac{1}{4}$,$\frac{1}{5}$.
| A. | 1组 | B. | 2组 | C. | 3组 | D. | 4组 |
7.要使分式$\frac{x+1}{{x}^{2}-1}$无意义,则x的值是( )
| A. | 1 | B. | -1 | C. | -1或1 | D. | 0 |

 如图,已知:梯形ABCD中,AD∥BC,EF过O点且平行于BC,求证:EO=FO.
如图,已知:梯形ABCD中,AD∥BC,EF过O点且平行于BC,求证:EO=FO. 如图,∠D=∠C=90°,AC=BD.求证:AD=BC.
如图,∠D=∠C=90°,AC=BD.求证:AD=BC. 已知,如图,在⊙O中,AB是直径,AD∥OC.
已知,如图,在⊙O中,AB是直径,AD∥OC.