题目内容
6. 已知,如图,在⊙O中,AB是直径,AD∥OC.
已知,如图,在⊙O中,AB是直径,AD∥OC.(1)求证:BC=CD;
(2)过O作OE⊥AD,若AE=3,∠OAC=30°,求⊙O的半径.
分析 (1)连接BC,CD,根据平行线的性质得到∠OCA=∠CAD,由等腰三角形的性质得到∠OCA=∠OAC,等量代换得到∠OAC=∠DAC,即可得到结论;
(2)根据垂直的定义得到∠AEO=90°,根据三角形的内角和得到∠AOE=30°,然后由30°角的直角三角形的性质即可得到结论.
解答 (1) 证明:连接BC,CD,
证明:连接BC,CD,
∵AD∥OC,
∴∠OCA=∠CAD,
∵OC=OA,
∴∠OCA=∠OAC,
∴∠OAC=∠DAC,
∴$\widehat{BC}=\widehat{CD}$,
∴BC=CD;
(2)解:∵OE⊥AD,
∴∠AEO=90°,
∵∠OAC=30°,
∴∠OAE=60°,
∴∠AOE=30°,
∵AE=3,
∴OA=2AE=6.
∴⊙O的半径是6.
点评 本题考查了平行线的性质,圆周角定理,含30°角的直角三角形的性质,熟记含30°角的直角三角形的性质是解题的关键.

练习册系列答案
 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案
相关题目
14.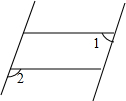 一只因损坏而倾斜的椅子,从背后看到的形状如图,其中两组对边的平行关系没有发生变化,若∠1=70°,则∠2的大小是( )
一只因损坏而倾斜的椅子,从背后看到的形状如图,其中两组对边的平行关系没有发生变化,若∠1=70°,则∠2的大小是( )
 一只因损坏而倾斜的椅子,从背后看到的形状如图,其中两组对边的平行关系没有发生变化,若∠1=70°,则∠2的大小是( )
一只因损坏而倾斜的椅子,从背后看到的形状如图,其中两组对边的平行关系没有发生变化,若∠1=70°,则∠2的大小是( )| A. | 70° | B. | 110° | C. | 60° | D. | 130° |
18.下列方程中配方中有错误的是( )
| A. | x2-4x-1=0化为(x-2)2=5 | B. | x2+6x+8=0化为(x+3)2=1 | ||
| C. | 2x2-7x-6=0化为${(x-\frac{7}{4})^2}=\frac{97}{8}$ | D. | 3x2-4x-2=0化为${(x-\frac{2}{3})^2}=\frac{10}{9}$ |
13. 如图,△ABC中,AC=16cm,DE为AB的垂直平分线,△BCE的周长为26cm,则BC的长为( )
如图,△ABC中,AC=16cm,DE为AB的垂直平分线,△BCE的周长为26cm,则BC的长为( )
 如图,△ABC中,AC=16cm,DE为AB的垂直平分线,△BCE的周长为26cm,则BC的长为( )
如图,△ABC中,AC=16cm,DE为AB的垂直平分线,△BCE的周长为26cm,则BC的长为( )| A. | 8 | B. | 9 | C. | 10 | D. | 16 |
 把二次函数y=$\frac{1}{2}$x2-3x+4配方成y=a(x-k)2+h的形式,并求出它的图象的顶点坐标、对称轴方程,并画出图象.
把二次函数y=$\frac{1}{2}$x2-3x+4配方成y=a(x-k)2+h的形式,并求出它的图象的顶点坐标、对称轴方程,并画出图象.