题目内容
15.一个等腰三角形的边长均满足方程x2-5x+6=0,则它的周长为6或7或8或9cm.分析 由等腰三角形的底和腰是方程x2-6x+8=0的两根,解此一元二次方程即可求得等腰三角形的腰与底边的长,注意需要分当2是等腰三角形的腰时与当4是等腰三角形的腰时讨论,然后根据三角形周长的求解方法求解即可.
解答 解:∵x2-5x+6=0,
∴(x-2)(x-3)=0,
解得:x=2或x=3,
∵等腰三角形的底和腰是方程x2-5x+6=0的两根,
∴当2是等腰三角形的腰时,2+2>3,能组成三角形,则这个三角形的周长为2+2+3=7;
当3是等腰三角形的腰时,3+3>2,则这个三角形的周长为3+3+2=8.
当边长为2的等边三角形,得出这个三角形的周长为2+2+2=6.
当边长为3的等边三角形,得出这个三角形的周长为3+3+3=9.
∴这个三角形的周长为6或7或8或9.
故答案是:6或7或8或9.
点评 此题考查了等腰三角形的性质,一元二次方程的解法.解题的关键是注意分类讨论你思想的应用.解一元二次方程,因式分解等知识点的理解和掌握,能把一元二次方程转换成一元一次方程是解此题的关键.

练习册系列答案
相关题目
5.若a、b都是非零的有理数,则式子$\frac{a}{|a|}+\frac{b}{|b|}$的所有可能的值共有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
6.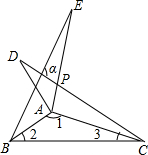 如图,△ABE、△ADC和△ABC分别是关于AB,AC边所在直线的轴对称图形,若∠1:∠2:∠3=7:2:1,则∠α的度数为( )
如图,△ABE、△ADC和△ABC分别是关于AB,AC边所在直线的轴对称图形,若∠1:∠2:∠3=7:2:1,则∠α的度数为( )
 如图,△ABE、△ADC和△ABC分别是关于AB,AC边所在直线的轴对称图形,若∠1:∠2:∠3=7:2:1,则∠α的度数为( )
如图,△ABE、△ADC和△ABC分别是关于AB,AC边所在直线的轴对称图形,若∠1:∠2:∠3=7:2:1,则∠α的度数为( )| A. | 90° | B. | 108° | C. | 110° | D. | 126° |
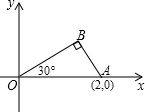 如图,将一块三角板放在平面直角坐标系中,已知∠AOB=30°,∠ABO=90°,且点A的坐标为(2,0).
如图,将一块三角板放在平面直角坐标系中,已知∠AOB=30°,∠ABO=90°,且点A的坐标为(2,0). 小鹏做了一个如图所示的程序图,按要求完成下列各小题.
小鹏做了一个如图所示的程序图,按要求完成下列各小题.