题目内容
10．
如图，∠D=∠C=90°，AC=BD．求证：AD=BC．
分析 根据HL证明Rt△ADB与Rt△ACB全等，进而证明AD=BC．
解答 证明：∵∠D=∠C=90°，
在Rt△ADB与Rt△ACB中，
$\left\{\begin{array}{l}{AC=BD}\\{AB=AB}\end{array}\right.$，
∴Rt△ADB≌Rt△ACB（HL），
∴AD=BC．
点评 本题考查了全等三角形的判定及性质；全等三角形的判定是重点，本题是道基础题，是对全等三角形的判定的训练．
练习册系列答案
相关题目
6．
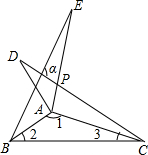如图，△ABE、△ADC和△ABC分别是关于AB，AC边所在直线的轴对称图形，若∠1：∠2：∠3=7：2：1，则∠α的度数为（ ）
如图，△ABE、△ADC和△ABC分别是关于AB，AC边所在直线的轴对称图形，若∠1：∠2：∠3=7：2：1，则∠α的度数为（ ）| A． | 90° | B． | 108° | C． | 110° | D． | 126° |
14．
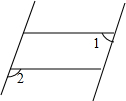一只因损坏而倾斜的椅子，从背后看到的形状如图，其中两组对边的平行关系没有发生变化，若∠1=70°，则∠2的大小是（ ）
一只因损坏而倾斜的椅子，从背后看到的形状如图，其中两组对边的平行关系没有发生变化，若∠1=70°，则∠2的大小是（ ）| A． | 70° | B． | 110° | C． | 60° | D． | 130° |
18．下列方程中配方中有错误的是（ ）
| A． | x2-4x-1=0化为（x-2）2=5 | B． | x2+6x+8=0化为（x+3）2=1 | ||
| C． | 2x2-7x-6=0化为${（x-\frac{7}{4}）^2}=\frac{97}{8}$ | D． | 3x2-4x-2=0化为${（x-\frac{2}{3}）^2}=\frac{10}{9}$ |