题目内容
10.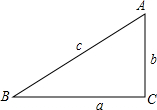 如图,在Rt△ABC中,∠C=90°,∠A、∠B、∠C所对的边分别用a、b、c表示,我们定义:锐角∠A的对边a与斜边c的比值$\frac{a}{c}$叫做∠A的正弦值,记为:sinA=$\frac{a}{c}$.如果某个直角三角形中,a=4,c=5,则∠A的正弦值为$\frac{4}{5}$,记为:sinA=$\frac{4}{5}$.如果某直角三角形中,∠A=60°,则sinA是( )
如图,在Rt△ABC中,∠C=90°,∠A、∠B、∠C所对的边分别用a、b、c表示,我们定义:锐角∠A的对边a与斜边c的比值$\frac{a}{c}$叫做∠A的正弦值,记为:sinA=$\frac{a}{c}$.如果某个直角三角形中,a=4,c=5,则∠A的正弦值为$\frac{4}{5}$,记为:sinA=$\frac{4}{5}$.如果某直角三角形中,∠A=60°,则sinA是( )| A. | 1 | B. | 0 | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
分析 在Rt△ABC中,∠C=90°,∠A=60°,∠A、∠B、∠C所对的边分别用a、b、c表示,则c=2b,利用勾股定理计算出a=$\sqrt{3}$b,然后根据正弦的定义求解.
解答 解:在Rt△ABC中,∠C=90°,∠A=60°,∠A、∠B、∠C所对的边分别用a、b、c表示,则c=2b,a=$\sqrt{{c}^{2}-{a}^{2}}$=$\sqrt{3}$b,
所以sinA=$\frac{a}{c}$=$\frac{\sqrt{3}b}{2b}$=$\frac{\sqrt{3}}{2}$.
故选D.
点评 本题考查了锐角三角函数的定义:在Rt△ABC中,∠C=90°,锐角∠A的对边a与斜边c的比值$\frac{a}{c}$叫做∠A的正弦值,记为:sinA=$\frac{a}{c}$.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
5.若a、b都是非零的有理数,则式子$\frac{a}{|a|}+\frac{b}{|b|}$的所有可能的值共有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
15.下列图中,中心对称图形的个数是( )


| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
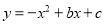 的图象经过坐标原点,与
的图象经过坐标原点,与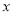 轴的另一个交点为A(-2,0).
轴的另一个交点为A(-2,0).
 ,其
,其
 把二次函数y=$\frac{1}{2}$x2-3x+4配方成y=a(x-k)2+h的形式,并求出它的图象的顶点坐标、对称轴方程,并画出图象.
把二次函数y=$\frac{1}{2}$x2-3x+4配方成y=a(x-k)2+h的形式,并求出它的图象的顶点坐标、对称轴方程,并画出图象.